题目内容
已知直线l过椭圆
+
=1的右焦点F2,与椭圆交于A、B两点,F1是它的左焦点,则△AF1B的周长是
| x2 |
| 16 |
| y2 |
| 8 |
16
16
.分析:根据椭圆的定义可得:|AF1|+|AF2|=2a,|BF1|+|BF2|=2a,并且|AF2|+|BF2|=|AB|,进而得到答案.
解答:解:根据题意结合椭圆的定义可得:|AF1|+|AF2|=2a=8,,并且|BF1|+|BF2|=2a=8,
又因为|AF2|+|BF2|=|AB|,
所以△AF1B的周长为:|AF1|+|BF1|+|AB|=|AF1|+|AF2|+|BF1|+|BF2|=16.
故答案为:16.
又因为|AF2|+|BF2|=|AB|,
所以△AF1B的周长为:|AF1|+|BF1|+|AB|=|AF1|+|AF2|+|BF1|+|BF2|=16.
故答案为:16.
点评:本题主要考查了椭圆的定义的应用,做题时要善于发现规律,进行转化.属于基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
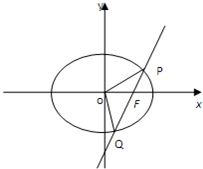 已知直线l过椭圆E:x2+2y2=2的右焦点F,且与E相交于P,Q两点.
已知直线l过椭圆E:x2+2y2=2的右焦点F,且与E相交于P,Q两点.
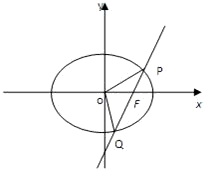 已知直线l过椭圆E:x2+2y2=2的右焦点F,且与E相交于P,Q两点.
已知直线l过椭圆E:x2+2y2=2的右焦点F,且与E相交于P,Q两点.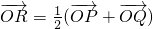 (O为原点),求点R的轨迹方程;
(O为原点),求点R的轨迹方程;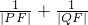 的值.
的值.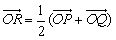 (O为原点),求点R的轨迹方程;
(O为原点),求点R的轨迹方程;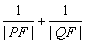 的值。
的值。 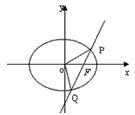
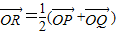 (O为原点),求点R的轨迹方程;
(O为原点),求点R的轨迹方程;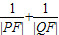 的值.
的值.