Question

（2013•北京）直线y=kx+m（m≠0）与椭圆W：

x2

4

+y2=1相交于A，C两点，O是坐标原点．
（Ⅰ）当点B的坐标为（0，1），且四边形OABC为菱形时，求AC的长；
（Ⅱ）当点B在W上且不是W的顶点时，证明：四边形OABC不可能为菱形．

Answer 1

分析：（I）先根据条件得出线段OB的垂直平分线方程为y=

1

2

，从而A、C的坐标为（±

3

，

1

2

），根据两点间的距离公式即可得出AC的长；
（II）欲证明四边形OABC不可能为菱形，只须证明若OA=OC，则A、C两点的横坐标相等或互为相反数．设OA=OC=r，则A、C为圆x²+y²=r²与椭圆W：

x2

4

+y2=1的交点，从而解得

3x2

4

=r2-1，则A、C两点的横坐标相等或互为相反数．于是结论得证．

解答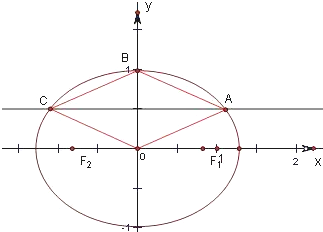：解：（I）∵点B的坐标为（0，1），当四边形OABC为菱形时，AC⊥OB，而B（0，1），O（0，0），
∴线段OB的垂直平分线为y=

1

2

，
将y=

1

2

代入椭圆方程得x=±

3

，
因此A、C的坐标为（±

3

，

1

2

），如图，
于是AC=2

3

．
（II）欲证明四边形OABC不可能为菱形，利用反证法，假设四边形OABC为菱形，则有OA=OC，
设OA=OC=r，则A、C为圆x²+y²=r²与椭圆W：

x2

4

+y2=1的交点，
故

3x2

4

=r2-1，x²=

4

3

（r²-1），则A、C两点的横坐标相等或互为相反数．
从而得到点B是W的顶点．这与题设矛盾．
于是结论得证．

点评：本题主要考查了椭圆的简单性质，直线与椭圆的位置关系，考查等价转化思想，属于基础题．