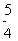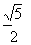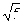题目内容
已知双曲线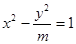 的虚轴长是实轴长的2倍,则实数
的虚轴长是实轴长的2倍,则实数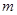 的值是( )
的值是( )
A.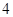 | B.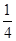 | C.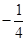 | D.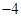 |
A
解析试题分析:利用双曲线方程,求出a,b,利用虚轴长是实轴长的2倍,推出m的值即可.根据题意,由于双曲线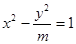 的虚轴长是实轴长的2倍,a=1,b=
的虚轴长是实轴长的2倍,a=1,b= 又虚轴长是实轴长的2倍,即2
又虚轴长是实轴长的2倍,即2 =4,所以m=4.故选A
=4,所以m=4.故选A
考点:双曲线的性质
点评:主要是考查了双曲线的几何性质的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知双曲线 的两条渐近线的夹角为
的两条渐近线的夹角为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. | B. | C. | D. |
抛物线 的焦点为
的焦点为 ,点
,点 为抛物线上的动点,点
为抛物线上的动点,点 为其准线上的动点,当
为其准线上的动点,当 为等边三角形时,其面积为
为等边三角形时,其面积为
A. | B.4 | C.6 | D.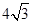 |
已知动点 在椭圆
在椭圆 上,若
上,若 点坐标为
点坐标为 ,
, ,且
,且 ,则
,则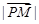 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
若双曲线 的离心率是2,则实数k的值是 ( )
的离心率是2,则实数k的值是 ( )
| A.—3 | B.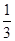 | C.3 | D.—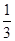 |
设 、
、 是双曲线
是双曲线 的左、右两个焦点,若双曲线右支上存在一点P,使
的左、右两个焦点,若双曲线右支上存在一点P,使 ,且
,且 ,则
,则 的值为( )
的值为( )
| A.2 | B. | C.3 | D. |
设 、
、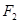 分别是椭圆
分别是椭圆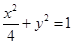 的左、右焦点,
的左、右焦点, 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且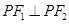 ,则点
,则点 的横坐标为
的横坐标为
A.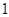 | B.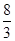 | C.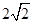 | D.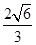 |
 的双曲线与圆
的双曲线与圆 的一个交点,则
的一个交点,则 = ( )
= ( )



 的一条渐近线与抛物线y=x
的一条渐近线与抛物线y=x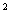 +1 只有一个公共点,则双曲线的离心率为( ).
+1 只有一个公共点,则双曲线的离心率为( ).