题目内容
已知抛物线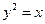 与直线
与直线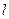 交于A,B两点(易于原点O),且以AB为直径的圆恰好过原点.
交于A,B两点(易于原点O),且以AB为直径的圆恰好过原点.
(1)求证:直线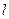 过定点.
过定点.
(2)求: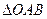 面积的最小值.
面积的最小值.
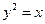 与直线
与直线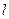 交于A,B两点(易于原点O),且以AB为直径的圆恰好过原点.
交于A,B两点(易于原点O),且以AB为直径的圆恰好过原点.(1)求证:直线
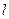 过定点.
过定点.(2)求:
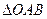 面积的最小值.
面积的最小值.证(1)设
易知直线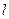 不平行于x轴,设
不平行于x轴,设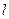 的方程为x=ky+b…………2分
的方程为x=ky+b…………2分
由AB为直径的圆过原点,得OA⊥OB…………3分

 ……………5分
……………5分
由 得
得 ……………6分
……………6分
由韦达定理得 ………7分
………7分
故: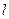 的方程为
的方程为 ,∴直线
,∴直线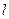 过定点(1,0)………8分
过定点(1,0)………8分
解(2):设C(1,0),则
 ……………10分
……………10分
 ………………12分
………………12分
∴当k=0时, 最小为1.…………13分
最小为1.…………13分

易知直线
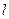 不平行于x轴,设
不平行于x轴,设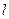 的方程为x=ky+b…………2分
的方程为x=ky+b…………2分由AB为直径的圆过原点,得OA⊥OB…………3分

 ……………5分
……………5分由
 得
得 ……………6分
……………6分由韦达定理得
 ………7分
………7分故:
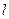 的方程为
的方程为 ,∴直线
,∴直线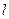 过定点(1,0)………8分
过定点(1,0)………8分解(2):设C(1,0),则

 ……………10分
……………10分 ………………12分
………………12分∴当k=0时,
 最小为1.…………13分
最小为1.…………13分同答案

练习册系列答案
相关题目


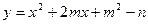 焦点坐标为(2001,2002),则它的顶点坐标为
焦点坐标为(2001,2002),则它的顶点坐标为  准线为l,l与x轴相交于点E,过F且倾斜角等于60°的直线与抛物线在x轴上方的部分相交于点A,AB⊥l,垂足为B,则四边形ABEF的面积等于()
准线为l,l与x轴相交于点E,过F且倾斜角等于60°的直线与抛物线在x轴上方的部分相交于点A,AB⊥l,垂足为B,则四边形ABEF的面积等于()



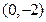 的直线与抛物线
的直线与抛物线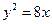 交于
交于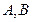 两点,若线段
两点,若线段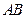 中点的横坐标为
中点的横坐标为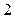 ,求
,求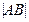 。
。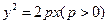 的焦点F作倾斜角为
的焦点F作倾斜角为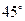 的直线交抛物线于A、B两点,若线段AB的长为8,则
的直线交抛物线于A、B两点,若线段AB的长为8,则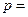 ________________
________________ 

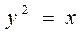 的焦点弦AB,求
的焦点弦AB,求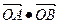 的值.
的值.