题目内容
(12分)等比数列 的各项均为正数,且
的各项均为正数,且 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)设 求数列
求数列 的前n项和
的前n项和 .
.
(1)  ;(2)
;(2)  .
.
【解析】
试题分析:(1)用基本量思想,结合等比数列等比中项的性质,构造首项和公比的关系式 ,
,
可解得 ,
, ;
;
(2)先求出
 ,再用拆项求和的方法就可以求出其前n项和
,再用拆项求和的方法就可以求出其前n项和 .
.
试题解析:(1)设数列 的公比为q,则由
的公比为q,则由 ,∴
,∴ ,
, q>0 ,∴
q>0 ,∴
由 得
得 ,∴
,∴ ,
,
故数列 的通项公式为
的通项公式为 ;
;
(2)
 ,
,
故 ,
,
∴ .
.
考点:等比数列,等差数列,拆项求和.
考点分析: 考点1:等比数列 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的不等式:
的不等式: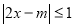 的整数解有且仅有一个值为2.
的整数解有且仅有一个值为2.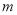 的值;
的值;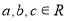 ,若
,若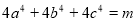 ,求
,求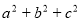 的最大值.
的最大值. 是第四象限的角,若
是第四象限的角,若 ,则
,则 ( )
( ) B.-
B.- D.-
D.-
 B.6
B.6
 D.18
D.18
 (x≠0)},B={x| x2-x-2≤0},则( )
(x≠0)},B={x| x2-x-2≤0},则( ) B B.B
B B.B A C.A=B D.A∩B=
A C.A=B D.A∩B=
 =_____.
=_____. (7<λ<9)的焦点坐标为( )
(7<λ<9)的焦点坐标为( ) ,0)
,0)  )
) ,右焦点为
,右焦点为 .若椭圆上存在一点
.若椭圆上存在一点 ,满足线段
,满足线段 相切于以椭圆的短轴为直径的圆,切点为线段
相切于以椭圆的短轴为直径的圆,切点为线段 的中点,则该椭圆的离心率为 ( )
的中点,则该椭圆的离心率为 ( ) B.
B. C.
C. D.
D.
 ,则
,则 .
.