题目内容
已知点P是椭圆 =1(xy≠0)上的动点,F1、F2为椭圆的左、右焦点,O为坐标原点,若M是∠F1PF2的角平分线上的一点,且
=1(xy≠0)上的动点,F1、F2为椭圆的左、右焦点,O为坐标原点,若M是∠F1PF2的角平分线上的一点,且 =0,则|
=0,则| |的取值范围是
|的取值范围是
- A.(0,3)
- B.(2
 ,3)
,3) - C.(0,4)
- D.(0,2
 )
)
D
分析:作出椭圆 =1的图象,通过观察图象可以发现,当点P在椭圆与y轴交点处时,点M与原点O重合,此时
=1的图象,通过观察图象可以发现,当点P在椭圆与y轴交点处时,点M与原点O重合,此时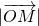 取最小值0.
取最小值0.
当点P在椭圆与x轴交点处时,点M与焦点F1重合,此时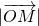 取最大值2
取最大值2 .由此能够得到|
.由此能够得到| |的取值范围.
|的取值范围.
解答: 解:如图,当点P在椭圆与y轴交点处时,点M与原点O重合,此时
解:如图,当点P在椭圆与y轴交点处时,点M与原点O重合,此时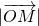 取最小值0.
取最小值0.
当点P在椭圆与x轴交点处时,点M与焦点F1重合,此时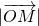 取最大值2
取最大值2 .
.
∵xy≠0,∴| |的取值范围是(0,2
|的取值范围是(0,2 ).
).
故选D.
点评:本题考查椭圆的性质,作出图象数形结合事半功倍.
分析:作出椭圆
 =1的图象,通过观察图象可以发现,当点P在椭圆与y轴交点处时,点M与原点O重合,此时
=1的图象,通过观察图象可以发现,当点P在椭圆与y轴交点处时,点M与原点O重合,此时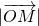 取最小值0.
取最小值0.当点P在椭圆与x轴交点处时,点M与焦点F1重合,此时
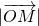 取最大值2
取最大值2 .由此能够得到|
.由此能够得到| |的取值范围.
|的取值范围.解答:
 解:如图,当点P在椭圆与y轴交点处时,点M与原点O重合,此时
解:如图,当点P在椭圆与y轴交点处时,点M与原点O重合,此时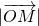 取最小值0.
取最小值0.当点P在椭圆与x轴交点处时,点M与焦点F1重合,此时
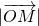 取最大值2
取最大值2 .
.∵xy≠0,∴|
 |的取值范围是(0,2
|的取值范围是(0,2 ).
).故选D.
点评:本题考查椭圆的性质,作出图象数形结合事半功倍.

练习册系列答案
相关题目
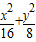 =1(xy≠0)上的动点,F1、F2为椭圆的左、右焦点,O为坐标原点,若M是∠F1PF2的角平分线上的一点,且
=1(xy≠0)上的动点,F1、F2为椭圆的左、右焦点,O为坐标原点,若M是∠F1PF2的角平分线上的一点,且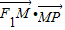 =0,则|
=0,则|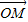 |的取值范围是( )
|的取值范围是( ) ,3)
,3) )
)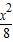 +
+ =1上的一点,F1、F2是椭圆的两个焦点,∠F1PF2=60°,则△F1PF2的面积是 .
=1上的一点,F1、F2是椭圆的两个焦点,∠F1PF2=60°,则△F1PF2的面积是 .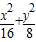 =1(xy≠0)上的动点,F1、F2为椭圆的左、右焦点,O为坐标原点,若M是∠F1PF2的角平分线上的一点,且
=1(xy≠0)上的动点,F1、F2为椭圆的左、右焦点,O为坐标原点,若M是∠F1PF2的角平分线上的一点,且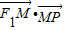 =0,则|
=0,则|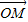 |的取值范围是( )
|的取值范围是( )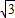 ,3)
,3)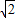 )
)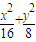 =1(xy≠0)上的动点,F1、F2为椭圆的左、右焦点,O为坐标原点,若M是∠F1PF2的角平分线上的一点,且
=1(xy≠0)上的动点,F1、F2为椭圆的左、右焦点,O为坐标原点,若M是∠F1PF2的角平分线上的一点,且 =0,则|
=0,则|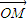 |的取值范围是( )
|的取值范围是( )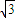 ,3)
,3) )
)