题目内容
已知点P是椭圆思路分析:![]() =
=![]() |PF1||PF2|sin30°;(2)能否求出|PF1|、|PF2|或整体求出|PF1|·|PF2|成为解本题的关键.
|PF1||PF2|sin30°;(2)能否求出|PF1|、|PF2|或整体求出|PF1|·|PF2|成为解本题的关键.
解:由椭圆方程知a=![]() ,b=2,
,b=2,
∴c=![]() =1.
=1.

又由椭圆定义知,|PF1|+|PF2|=2a=2![]() . ①
. ①
由余弦定理知,|PF1|2+|PF2|2-2|PF1|·|PF2|cos30°=|F1F2|2=4. ②
①2-②得(2+![]() )|PF1|·|PF2|=16,
)|PF1|·|PF2|=16,
∴|PF1|·|PF2|=16(2-![]() ).
).
∴![]() =
=![]() |PF1|·|PF2|sin30°=8-4
|PF1|·|PF2|sin30°=8-4![]() .
.

练习册系列答案
相关题目
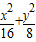 =1(xy≠0)上的动点,F1、F2为椭圆的左、右焦点,O为坐标原点,若M是∠F1PF2的角平分线上的一点,且
=1(xy≠0)上的动点,F1、F2为椭圆的左、右焦点,O为坐标原点,若M是∠F1PF2的角平分线上的一点,且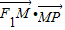 =0,则|
=0,则|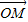 |的取值范围是( )
|的取值范围是( ) ,3)
,3) )
)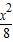 +
+ =1上的一点,F1、F2是椭圆的两个焦点,∠F1PF2=60°,则△F1PF2的面积是 .
=1上的一点,F1、F2是椭圆的两个焦点,∠F1PF2=60°,则△F1PF2的面积是 .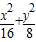 =1(xy≠0)上的动点,F1、F2为椭圆的左、右焦点,O为坐标原点,若M是∠F1PF2的角平分线上的一点,且
=1(xy≠0)上的动点,F1、F2为椭圆的左、右焦点,O为坐标原点,若M是∠F1PF2的角平分线上的一点,且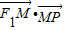 =0,则|
=0,则|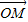 |的取值范围是( )
|的取值范围是( )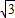 ,3)
,3)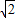 )
)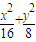 =1(xy≠0)上的动点,F1、F2为椭圆的左、右焦点,O为坐标原点,若M是∠F1PF2的角平分线上的一点,且
=1(xy≠0)上的动点,F1、F2为椭圆的左、右焦点,O为坐标原点,若M是∠F1PF2的角平分线上的一点,且 =0,则|
=0,则|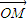 |的取值范围是( )
|的取值范围是( )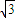 ,3)
,3) )
)