题目内容

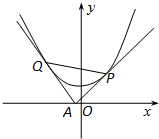
椭圆C的中心在原点O，焦点在x轴，它的短轴长为2，过焦点与x轴垂直的直线与椭圆C相交于A，B两点且|AB|=1．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过定点N（1，0）的直线l交椭圆C于C、D两点，交y轴于点P，若
PC
=λ1
CN
，
PD
=λ2
DN
，求证：λ1+λ2为定值．
（Ⅰ）设椭圆方程为
x2
a2
+
y2
b2
=1．
令x=-c，代入椭圆方程得，y=±
b2
a
．
所以2×
b2
a
=1，2b=2，
解得a=2，b=1．
∴椭圆的标准方程为
x2
4
+y2=1；
（Ⅱ）设直线l的方程为x=my-1，则P点坐标为（0，
1
m
）
设C（x1，y1），D（x2，y2）
联立直线与椭圆的方程
x=my-1
x2
4
+y2=1
，得（m2+4）y2-2my-3=0，
∴y1+y2=
2m
m2+4
，y1y2=
-3
m2+4

又∵
PC
=λ1
CN
，
PD
=λ2
DN
，
∴λ1=
1
m
-y1
y1
，λ2=
1
m
-y2
y2
，
∴λ1+λ2=
1
m
-y1
y1
+
1
m
-y2
y2
=
1
my1
+
1
my2
-2=
y1+y2
my1y2
-2=-
2
3
-2=-
8
3

即λ1+λ2为定值
练习册系列答案
相关题目
设椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右顶点分别为A（-
2
，0）、B（
2
，0），离心率e=
2
2
．过该椭圆上任一点P作PQ⊥x轴，垂足为Q，点C在QP的延长线上，且|PC|=（
2
-1）|PQ|．
（1）求椭圆的方程；
（2）求动点C的轨迹E的方程；
（3）设直线MN过椭圆的右焦点与椭圆相交于M、N两点，且|MN|=
8
2
7
，求直线MN的方程．
如图，已知圆C1的方程为(x-2)2+(y-1)2=
20
3
，椭圆C2的方程为
x2
a2
+
y2
b2
=1（a＞b＞0），C2的离心率为
2
2
，如果C1与C2相交于A、B两点，且线段AB恰为圆C1的直径，求直线AB的方程和椭圆C2的方程．
过（2，0）点且倾斜角为60°的直线与椭圆
x2
5
+
y2
3
=1相交于A，B两点，则AB中点的坐标为______．
过x轴上动点A（a，0）引抛物线y=x2+1的两条切线AP、AQ，P、Q为切点．
（1）若切线AP，AQ的斜率分别为k1和k2，求证：k1•k2为定值，并求出定值；
（2）求证：直线PQ恒过定点，并求出定点坐标；
（3）当
S△APO
PQ
最小时，求
AQ
•
AP
的值．
已知直线y=kx-1与双曲线x2-y2=4没有公共点，则实数k的取值范围为______．
已知椭圆C1：
x2
4
+
y2
3
=1和抛物线C2：y2=2px（p＞0），过点M（1，0）且倾斜角为
π
3
的直线与抛物线交于A、B，与椭圆交于C、D，当|AB|：|CD|=5：3时，求p的值．
已知点P(-1，
3
2
)是椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）上一点，F1、F2分别是椭圆E的左、右焦点，O是坐标原点，PF1⊥x轴．
（1）求椭圆E的方程；
（2）设A、B是椭圆E上两个动点，是否存在λ，满足
PA
+
PB
=λ
PO
（0＜λ＜4，且λ≠2），且M（2，1）到AB的距离为
5
？若存在，求λ值；若不存在，说明理由．
斜率为2的直线l与双曲线
x2
3
-
y2
2
=1交于A，B两点，且|AB|=4，求直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网