题目内容
在△ 中,角
中,角 ,
, ,
, ,的对边分别为
,的对边分别为 .
.
已 知向量 ,
,  ,
, .
.
(1)求 的值;
的值;
(2)若 ,求△
,求△ 周长的范围.
周长的范围.
(1) (2)
(2)
解析试题分析:根据题意,由于 ,
,  ,
, ,则可知有
,则可知有 ,故有
,故有
(2)因为 ,那么则△
,那么则△ 周长L=a+b+c=
周长L=a+b+c= ,则可以变形得到其表达式为
,则可以变形得到其表达式为 ,故可知范围是
,故可知范围是
考点:向量的数量积,三角形的余弦定理
点评:解决的关键是根据向量的数量积得到角A,然后借助于余弦定理和均值不等式来求解范围,属于基础题。

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 .
. 的最大值及最小正周期;
的最大值及最小正周期; ,
, ,求
,求 的值.
的值. .
. 的最大值,并求取得最大值时角A、B的大小.
的最大值,并求取得最大值时角A、B的大小. 的最大值.
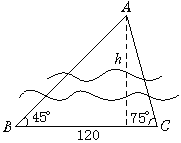
的最大值.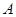 相距20
相距20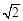 海里的B处有一货船正以匀速直线 行驶,20分钟后又测得该船只位于观测站A北偏东
海里的B处有一货船正以匀速直线 行驶,20分钟后又测得该船只位于观测站A北偏东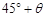
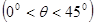 的C处,
的C处,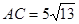 .在离观测站A的正南方某处E,
.在离观测站A的正南方某处E,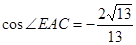
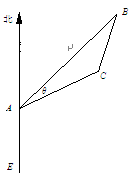
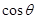 ; (2)求该船的行驶速度v(海里/小时);
; (2)求该船的行驶速度v(海里/小时); 中,若
中,若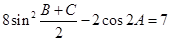 。
。 的大小;
的大小; ,
, ,求
,求 ,
, 的值。
的值。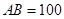 米,如图,同时也能测量出
米,如图,同时也能测量出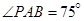 ,
,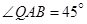 ,
,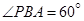 ,
,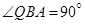 ,则P、Q两棵树和A、P两棵树之间的距离各为多少?
,则P、Q两棵树和A、P两棵树之间的距离各为多少?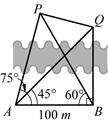
 中,角
中,角 的对边分别为
的对边分别为 ,
,
 ,
,
 ,且
,且
 的值; (2) 若
的值; (2) 若 ,
,  , 求
, 求 的值.
的值.