题目内容
 如图,在等腰直角△ABC中,点D是斜边BC的中点,过点D的直线分别交AB,AC于点M,N,若
如图,在等腰直角△ABC中,点D是斜边BC的中点,过点D的直线分别交AB,AC于点M,N,若| AM |
| AB |
| AN |
| AC |
3+2
| 2 |
3+2
.| 2 |
分析:利用三角形的直角建立坐标系,求出各个点的坐标,有条件求出M和N坐标,则由截距式直线方程求出MN的直线方程,根据点D(1,1)在直线上,求出x,y的关系式,利用基本不等式求出2x+4y的最小值
解答:解:以AC、AB为a,b轴建立直角坐标系,设等腰直角△ABC的腰长为2,
则D点坐标为(1,1),B(0,2)、C(2,0),
∵
=x
,
=y
,
∴点M坐标为(0,2x),点N的坐标为(2y,0)
∴直线MN的方程为
+
=1
∵直线MN过点D(1,1),
∴
+
=1
∴
+
=2
则2x+4y=(
+
)x+2•(
+
)y=3+(
+
)≥3+2
故答案为:3+2
则D点坐标为(1,1),B(0,2)、C(2,0),
∵
| AM |
| AB |
| AN |
| AC |
∴点M坐标为(0,2x),点N的坐标为(2y,0)
∴直线MN的方程为
| a |
| 2x |
| b |
| 2y |
∵直线MN过点D(1,1),
∴
| 1 |
| 2x |
| 1 |
| 2y |
∴
| 1 |
| x |
| 1 |
| y |
则2x+4y=(
| 1 |
| x |
| 1 |
| y |
| 1 |
| x |
| 1 |
| y |
| x |
| y |
| 2y |
| x |
| 2 |
故答案为:3+2
| 2 |
点评:本题的考查了利用向量的坐标运算求最值问题,需要根据图形的特征建立坐标系,转化为几何问题,根据条件求出两数的和,再由基本不等式求出它们的积的最大值,注意验证三个条件:一正二定三相等,考查了转化思想.

练习册系列答案
相关题目
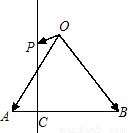
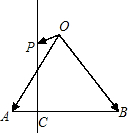 如图,在等腰直角△ABO中,设
如图,在等腰直角△ABO中,设 如图,在等腰直角三角形ABC中,则AM<AC的概率为( )
如图,在等腰直角三角形ABC中,则AM<AC的概率为( ) 为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,
为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,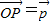 ,则
,则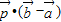 =( )
=( )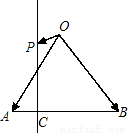
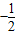



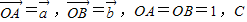 为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,
为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,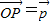 ,则
,则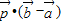 =( )
=( )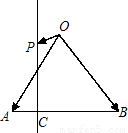
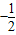

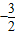

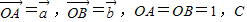 为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,
为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,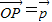 ,则
,则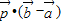 =( )
=( )