题目内容
要在墙上开一个上部为半圆,下部为矩形的窗户(如图所示),在窗框总长度为l的条件下,
(1)请写出窗户的面积S与圆的直径x的函数关系;
(2)要使窗户透光面积最大,窗户应具有怎样的尺寸?并写出最大值.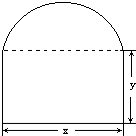
(1)请写出窗户的面积S与圆的直径x的函数关系;
(2)要使窗户透光面积最大,窗户应具有怎样的尺寸?并写出最大值.

(1)设半圆的直径为x,矩形的高度为y,
窗户透光面积为S,
则窗框总长l=
+x+2y
∴y=
S=
x2 +xy=
x2+
•x
∴S=-
x2+
x (0<x<
)
(2)S=-
(x-
)2+
当x=
时,Smax=
此时,y=
=
…7分
答:窗户中的矩形高为
,且半径等于矩形的高时,窗户的透光面积最大.
窗户透光面积为S,
则窗框总长l=
| πx |
| 2 |
∴y=
| 2l-(2+π)x |
| 4 |
S=
| π |
| 8 |
| π |
| 8 |
| 2l-(2+π)x |
| 4 |
∴S=-
| 4+π |
| 8 |
| l |
| 2 |
| 2l |
| π+2 |
(2)S=-
| 4+π |
| 8 |
| 2l |
| 4+π |
| l2 |
| 2(4+π) |
当x=
| 2l |
| 4+π |
| l2 |
| 2(4+π) |
此时,y=
| l |
| 4+π |
| x |
| 2 |
答:窗户中的矩形高为
| l |
| 4+π |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
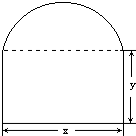 要在墙上开一个上部为半圆,下部为矩形的窗户(如图所示),在窗框总长度为l的条件下,
要在墙上开一个上部为半圆,下部为矩形的窗户(如图所示),在窗框总长度为l的条件下, (7分)要在墙上开一个上部为半圆,下部为矩形的窗户
(7分)要在墙上开一个上部为半圆,下部为矩形的窗户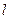 的条件下,
的条件下,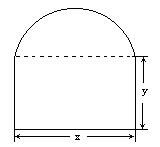
 出窗户的面积
出窗户的面积 与圆的直径
与圆的直径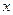 的函数关系;
的函数关系;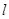 的条件下,
的条件下,
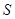 与圆的直径
与圆的直径 的函数关系;
的函数关系;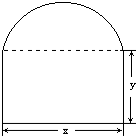 要在墙上开一个上部为半圆,下部为矩形的窗户(如图所示),在窗框总长度为l的条件下,
要在墙上开一个上部为半圆,下部为矩形的窗户(如图所示),在窗框总长度为l的条件下,