题目内容
定义在R上的函数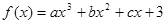 同时满足以下条件:
同时满足以下条件:
①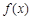 在(0,1)上是减函数,在(1,+∞)上是增函数;
在(0,1)上是减函数,在(1,+∞)上是增函数;
②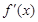 是偶函数;
是偶函数;
③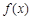 在x=0处的切线与直线y=x+2垂直.
在x=0处的切线与直线y=x+2垂直.
(1)求函数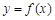 的解析式;
的解析式;
(2)设g(x)=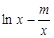 ,若存在实数x∈[1,e],使g(x)<
,若存在实数x∈[1,e],使g(x)<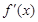 ,求实数m的取值范围。
,求实数m的取值范围。
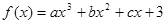 同时满足以下条件:
同时满足以下条件:①
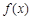 在(0,1)上是减函数,在(1,+∞)上是增函数;
在(0,1)上是减函数,在(1,+∞)上是增函数;②
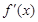 是偶函数;
是偶函数;③
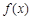 在x=0处的切线与直线y=x+2垂直.
在x=0处的切线与直线y=x+2垂直.(1)求函数
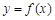 的解析式;
的解析式;(2)设g(x)=
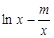 ,若存在实数x∈[1,e],使g(x)<
,若存在实数x∈[1,e],使g(x)<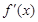 ,求实数m的取值范围。
,求实数m的取值范围。(1) f(x)=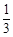 x3 x+3, (2) m>2e e3
x3 x+3, (2) m>2e e3
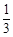 x3 x+3, (2) m>2e e3
x3 x+3, (2) m>2e e3试题分析:(1)三个条件,三个未知数,本题就是通过条件列方程组解参数,第一个条件说的是单调性,实质是导数,即
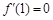 ,3a+2b+c=0;第二个条件是函数的奇偶性,利用
,3a+2b+c=0;第二个条件是函数的奇偶性,利用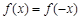 恒成立即可,b=0;第三个条件是导数几何意义,即
恒成立即可,b=0;第三个条件是导数几何意义,即 , c= 1 ;因此
, c= 1 ;因此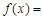
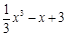 ;(2)存在型问题,转化为函数最值,首先进行变量分离,即m>xlnx x3+x,然后求函数M(x)=xlnx x3+x在[1,e]上最小值,这又要利用导数研究函数M(x)在[1,e]上的单调性,分析得为M(x)在[1,e]上递减,所以M(x)最小值为M(e)=2e e3于是有m>2e e3
;(2)存在型问题,转化为函数最值,首先进行变量分离,即m>xlnx x3+x,然后求函数M(x)=xlnx x3+x在[1,e]上最小值,这又要利用导数研究函数M(x)在[1,e]上的单调性,分析得为M(x)在[1,e]上递减,所以M(x)最小值为M(e)=2e e3于是有m>2e e3试题解析:解:(1)f′(x)=3ax2+2bx+c,∵f(x)在(0,1)上是减函数,在(1,+∞)上是增函数,
∴f′(1)=3a+2b+c=0 ①
由f′(x)是偶函数得:b=0 ②
又f(x)在x=0处的切线与直线y=x+2垂直,f′(0)=c= 1 ③
由①②③得:a=
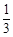 ,b=0,c= 1,即
,b=0,c= 1,即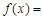
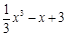 . 4分
. 4分(2)由已知得:存在实数x∈[1,e],使lnx
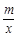 <x2 1
<x2 1即存在x∈[1,e],使m>xlnx x3+x 6分
设M(x)=xlnx x3+x,x∈[1,e],则M′(x)=lnx 3x2+2 8分
设H(x)=lnx 3x2+2,则H′(x)=
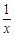 6x=
6x=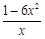 10分
10分∴M(x)在[1,e]上递减,
∵x∈[1,e],∴H′(x)<0,即H(x)在[1,e]上递减
于是,H(x)≤H(1),即H(x)≤ 1<0,即M′(x)<0
∴M(x)≥M(e)=2e e3
于是有m>2e e3为所求. 12分

练习册系列答案
相关题目
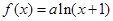 ,
,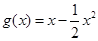 ,
,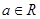
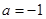 ,求曲线
,求曲线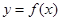 在
在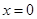 处的切线方程;
处的切线方程;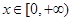 ,都有
,都有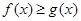 恒成立,求
恒成立,求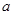 的最小值;
的最小值;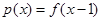 ,
,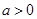 ,若
,若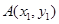 ,
,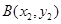 为曲线
为曲线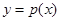 的两个不同点,满足
的两个不同点,满足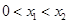 ,且
,且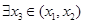 ,使得曲线
,使得曲线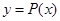 在
在 处的切线与直线AB平行,求证:
处的切线与直线AB平行,求证: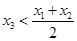
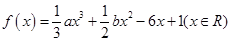 ,
,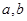 为实常数。
为实常数。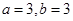 时,求函数
时,求函数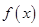 的极大、极小值;
的极大、极小值;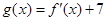 ,其中
,其中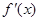 是
是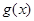 的导函数为
的导函数为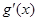 ,
,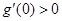 ,
,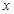 轴有且仅有一个公共点,求
轴有且仅有一个公共点,求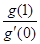 的最小值.
的最小值.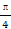 ,则4x与3sin2x的大小关系是( )
,则4x与3sin2x的大小关系是( )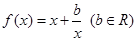 的导函数在区间
的导函数在区间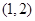 上有零点,则
上有零点,则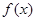 在下列区间单调递增的是( )
在下列区间单调递增的是( )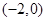
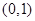
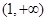
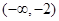
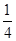
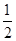
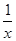 -1.
-1. 的导数
的导数 .
.