题目内容
如图,△ABC为正三角形,CE⊥平面ABC,BD∥CE,且CE=AC=2BD,M是AE的中点,求证:①DE=DA;②平面BDM⊥平面ECA;③平面DEA⊥平面ECA.
证明:①取EC的中点F,连结DF.
∵CE⊥平面ABC,
∴CE⊥BC.易知DF∥BC,∴CE⊥DF.
∵BD∥CE,∴BD⊥平面ABC.
在Rt△EFD和Rt△DBA中,
∵EF=![]() CE=DB,DF=BC=AB,
CE=DB,DF=BC=AB,
∴Rt△EFD≌Rt△DBA,故DE=AD.
②取AC的中点N,连结MN、BN,则MN![]() CF.
CF.
∵BD![]() ,∴MN
,∴MN![]() BD,∴N∈平面BDM.
BD,∴N∈平面BDM.
∵EC⊥平面ABC,∴EC⊥BN.
又∵AC⊥BN,∴BN⊥平面ECA.
又∵BN![]() 平面MNBD,∴平面BDM⊥平面ECA.
平面MNBD,∴平面BDM⊥平面ECA.
③∵DM∥BN,BN⊥平面ECA,∴DM⊥平面ECA.
又∵DM![]() 平面DEA,∴平面DEA⊥平面ECA.
平面DEA,∴平面DEA⊥平面ECA.
点评:本题涉及线面垂直、面面垂直的性质和判定,这里证明的关键是BN⊥平面ECA,在这里应充分体会线线垂直、线面垂直与面面垂直的关系.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
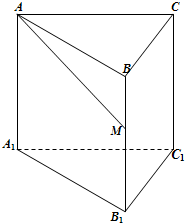 如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.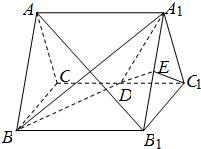 如图,已知正三棱柱ABC-A1B1C1的所有棱长都是2,D、E分别为CC1、A1B1的中点.
如图,已知正三棱柱ABC-A1B1C1的所有棱长都是2,D、E分别为CC1、A1B1的中点. 如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点.
如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点. 如图,已知正三棱柱ABC-A1B1C1的底面边长为
如图,已知正三棱柱ABC-A1B1C1的底面边长为 (2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.
(2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.