题目内容
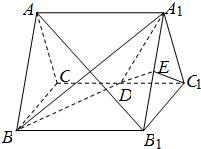 如图,已知正三棱柱ABC-A1B1C1的所有棱长都是2,D、E分别为CC1、A1B1的中点.
如图,已知正三棱柱ABC-A1B1C1的所有棱长都是2,D、E分别为CC1、A1B1的中点.(1)求证C1E∥平面A1BD;
(2)求证AB1⊥平面A1BD;
(3)求三棱锥A1-C1DE的体积.
分析:(1)要证C1E∥平面A1BD;只须证明直线平行平面内的一条直线,图中DF即可.
(2)要证AB1⊥平面A1BD;只须证明只须垂直平面内的两条相交直线A1B、DF 即可,前者利用正方形证明,后者△A1BD说明是等腰三角形.
(3)求三棱锥A1-C1DE的体积.利用等底面面积等高体积相等,转化为D-A1EC1的体积,再转化为D-A1B1C1的体积求解即可.
(2)要证AB1⊥平面A1BD;只须证明只须垂直平面内的两条相交直线A1B、DF 即可,前者利用正方形证明,后者△A1BD说明是等腰三角形.
(3)求三棱锥A1-C1DE的体积.利用等底面面积等高体积相等,转化为D-A1EC1的体积,再转化为D-A1B1C1的体积求解即可.
解答: 解:(1)设AB1与A1B相交于F,连EF,DF.则EF为△AA1B1的中位线,∴EF∥=
解:(1)设AB1与A1B相交于F,连EF,DF.则EF为△AA1B1的中位线,∴EF∥=
A1A.
∵C1D∥=
A1A,∴EF∥=C1D,则四边形EFDC1为平行四边形,∴DF∥C1E.
∵C1E?平面A1BD,DF?平面A1BD,∴C1E∥平面A1BD.
(2)取BC的中点H,连接AH,B1H,
由正三棱柱ABC-A1B1C1,知AH⊥BC,
∵B1B⊥平面ABC,∴B1B⊥AH.∵B1B∩BC=B,∴AH⊥平面B1BCC1.∴AH⊥BD.
在正方形B1BCC1中,∵tan∠BB1H=tan∠CBD=
,∴∠BB1H=∠CBD.则B1H⊥BD.
∵AH⊥∩B1H=H,∴BD⊥平面AHB1.∴BD⊥AB1.
在正方形A1ABB1中,∵A1B⊥AB1.而A1B∩BD=B,∴AB1⊥平面A1BD.
(3)∵E为AB的中点,∴VA1-C1DE=VD-A1EC1=
VD-A1B1C1=
×
×
×22×1=
.
 解:(1)设AB1与A1B相交于F,连EF,DF.则EF为△AA1B1的中位线,∴EF∥=
解:(1)设AB1与A1B相交于F,连EF,DF.则EF为△AA1B1的中位线,∴EF∥=| 1 |
| 2 |
∵C1D∥=
| 1 |
| 2 |
∵C1E?平面A1BD,DF?平面A1BD,∴C1E∥平面A1BD.
(2)取BC的中点H,连接AH,B1H,
由正三棱柱ABC-A1B1C1,知AH⊥BC,
∵B1B⊥平面ABC,∴B1B⊥AH.∵B1B∩BC=B,∴AH⊥平面B1BCC1.∴AH⊥BD.
在正方形B1BCC1中,∵tan∠BB1H=tan∠CBD=
| 1 |
| 2 |
∵AH⊥∩B1H=H,∴BD⊥平面AHB1.∴BD⊥AB1.
在正方形A1ABB1中,∵A1B⊥AB1.而A1B∩BD=B,∴AB1⊥平面A1BD.
(3)∵E为AB的中点,∴VA1-C1DE=VD-A1EC1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| ||
| 4 |
| ||
| 6 |
点评:本题考查棱柱的结构特征,考查棱柱、棱锥的体积,考查转化思想,是中档题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
 如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点.
如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点. 如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为
如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为 如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点.
如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点. 如图,已知正三棱柱ABC-A1B1C1,D是AC的中点,
如图,已知正三棱柱ABC-A1B1C1,D是AC的中点, (2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为
(2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为