题目内容
设 .
.
(Ⅰ)若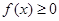 对一切
对一切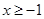 恒成立,求
恒成立,求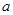 的取值范围;
的取值范围;
(Ⅱ)设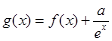 ,且
,且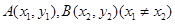 是曲线
是曲线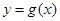 上任意两点,若对任意的
上任意两点,若对任意的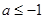 ,直线AB的斜率恒大于常数
,直线AB的斜率恒大于常数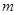 ,求
,求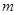 的取值范围;
的取值范围;
(Ⅲ)求证: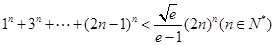 .
.
(Ⅰ)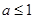 ;(Ⅱ)
;(Ⅱ)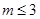 ;(Ⅲ)详见解析
;(Ⅲ)详见解析
解析试题分析:(Ⅰ)
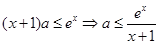
∴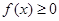 对一切
对一切 恒成立等价于
恒成立等价于 恒成立.
恒成立.
这只要求出函数 的最小值即可.
的最小值即可.
(Ⅱ)直线的斜率为: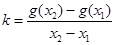
由题设有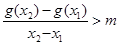 ,不妨设
,不妨设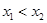
则
这样问题转化为函数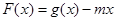 ,在
,在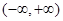 上单调递增
上单调递增
所以 恒成立,即对任意
恒成立,即对任意 ,
,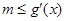 恒成立
恒成立
这样只需求出 的最小值即可.
的最小值即可.
(Ⅲ)不等式 可变为
可变为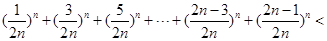
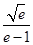
由(Ⅰ) 知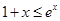 (
(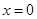 时取等号),在此不等式中
时取等号),在此不等式中
取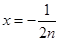 得:
得: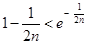 变形得:
变形得:
取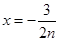 得:
得: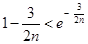 变形得:
变形得:
取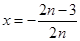 得:
得: 变形得:
变形得: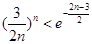
取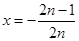 得:
得: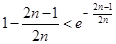 变形得:
变形得: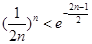
将以上不等式相加即可得证.
试题解析:(Ⅰ)
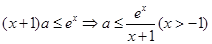
令 ,则
,则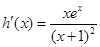
由 得
得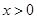 .所以
.所以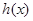 在
在 上单调递增,
上单调递增, 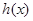 在
在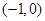 单调递减.
单调递减.
所以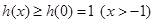
由此得: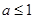
又 时,
时,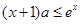 即为
即为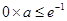 此时
此时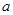 取任意值都成立
取任意值都成立
综上得: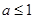
(II)由题设得,直线AB的斜率满足: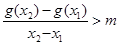 ,
,
不妨设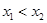 ,则
,则 即:
即:
令函数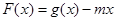 ,则由以上不等式知:
,则由以上不等式知: 在
在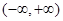 上单调递增,
上单调递增,
所以 恒成立
恒成立
所以,对任意 ,
,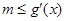 恒成立
恒成立
又
 =
=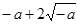
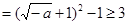
故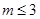
(Ⅲ)由(Ⅰ) 知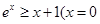 时取等号),
时取等号),
取 ,
,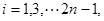 得
得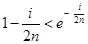
即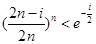 累加得
累加得
练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 ,数列
,数列 ,满足0<
,满足0< <1,
<1, ,数列
,数列 满足
满足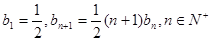 ,
, 的单调区间;
的单调区间; <
< <1;
<1; 且
且 ,则当n≥2时,求证:
,则当n≥2时,求证: >
>
 为函数
为函数 图象上一点,
图象上一点, 为坐标原点,记直线
为坐标原点,记直线 的斜率
的斜率 .
. 在区间
在区间 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
 .
. 的单调区间;
的单调区间; ,若
,若 在
在 上单调递增,求
上单调递增,求 的取值范围.
的取值范围. ,
, ,
, ,点A、B为函数
,点A、B为函数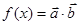 的相邻两个零点,AB=π.
的相邻两个零点,AB=π. 的值;
的值;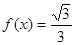 ,
,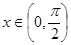 ,求
,求 的值;
的值; 在区间
在区间 上的单调递减区间.
上的单调递减区间. (其中
(其中 ),且方程
),且方程 的两个根分别为
的两个根分别为 、
、 .
. 且曲线
且曲线 过原点时,求
过原点时,求 的解析式;
的解析式; 无极值点,求
无极值点,求 的取值范围.
的取值范围. x
x -ax+(a-1)
-ax+(a-1) ,
, 。
。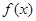 的单调性;(2)若
的单调性;(2)若 ,设
,设 ,
, ,x
,x

 ,x
,x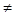 x
x .
.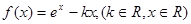
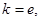 试确定函数
试确定函数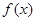 的单调区间;
的单调区间;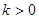 ,且对于任意
,且对于任意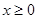 ,
,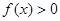 恒成立,求实数
恒成立,求实数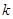 的取值范围;
的取值范围;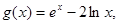 若至少存在一个实数
若至少存在一个实数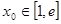 ,使
,使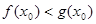 成立,求实数
成立,求实数 .
. .
. 在
在 上是增函数,求
上是增函数,求 的取值范围.
的取值范围.