题目内容
已知 为函数
为函数 图象上一点,
图象上一点, 为坐标原点,记直线
为坐标原点,记直线 的斜率
的斜率 .
.
(1)若函数 在区间
在区间 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围;
(2)当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)求证:
(1)实数 的取值范围是
的取值范围是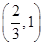 ;(2)实数
;(2)实数 的取值范围是
的取值范围是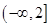 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)先利用导数求出函数 的解析式,并利用导数求出函数
的解析式,并利用导数求出函数 的极值点,并将极值点限制在区间
的极值点,并将极值点限制在区间 内,得出有关
内,得出有关 的不等式,求解出实数
的不等式,求解出实数 的取值范围;(2)利用参数分离法将问题
的取值范围;(2)利用参数分离法将问题 在区间
在区间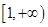 上恒成立转化为不等式
上恒成立转化为不等式 在区间
在区间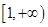 上恒成立,构造新函数
上恒成立,构造新函数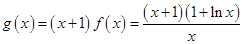 ,从而将问题转化为
,从而将问题转化为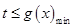 ,借助导数求函数
,借助导数求函数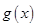 的最小值,从而得到实数
的最小值,从而得到实数 的取值范围;(3)取
的取值范围;(3)取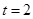 ,由(2)中的结论
,由(2)中的结论 ,即
,即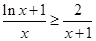 在
在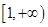 上恒成立,从而得到
上恒成立,从而得到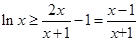 在
在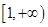 上恒成立,,令
上恒成立,,令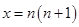 ,代入上述不等式得到
,代入上述不等式得到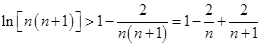 ,结合累加法即可证明不等式
,结合累加法即可证明不等式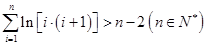 .
.
试题解析:(1)由题意 ,
,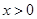 1分
1分
所以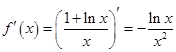 2分
2分
当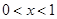 时,
时,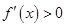 ;当
;当 时,
时,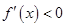 .
.
所以 在
在 上单调递增,在
上单调递增,在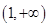 上单调递减,
上单调递减,
故 在
在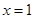 处取得极大值. 3分
处取得极大值. 3分
因为函数 在区间
在区间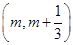 (其中
(其中 )上存在极值,
)上存在极值,
所以 ,得
,得 .即实数
.即实数 的取值范围是
的取值范围是 . 4分
. 4分
(2)由 得
得 ,令
,令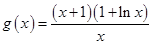 ,
,
则 . 6分
. 6分
令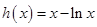 ,则
,则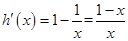 ,
,
因为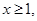 所以
所以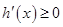 ,故
,故 在
在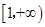 上单调递增. 7分
上单调递增. 7分
所以 ,从而
,从而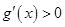
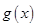 在
在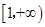 上单调递增,
上单调递增, 
所以实数 的取值范围是
的取值范围是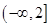 . 9分
. 9分
(3)由(2) 知 恒成立,
恒成立,
即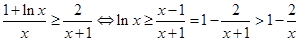 11分
11分
令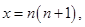 则
则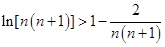 , 12分
, 12分
所以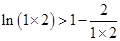 ,
,

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目

 在
在 是增函数,求
是增函数,求 的取值范围;
的取值范围; ,对于函数
,对于函数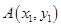 ,
, ,其中
,其中 ,直线
,直线 的斜率为
的斜率为 ,记
,记 ,若
,若 求证:
求证: .
. ,
, 且
且
 的图象在它们与坐标轴交点处的切线互相平行.
的图象在它们与坐标轴交点处的切线互相平行. 的值;
的值; 使不等式
使不等式 成立,求实数
成立,求实数 的取值范围;
的取值范围;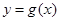 公共定义域内的任意实数
公共定义域内的任意实数 ,我们把
,我们把
 的值称为两函数在
的值称为两函数在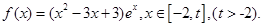
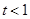 时,求函数
时,求函数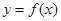 的单调区间;
的单调区间;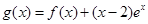 ,试问函数
,试问函数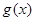 在
在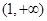 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.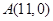 ,直线
,直线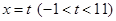 与函数
与函数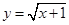 的图象交于点
的图象交于点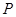 ,与
,与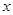 轴交于点
轴交于点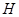 ,记
,记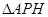 的面积为
的面积为 .
.
 ,函数
,函数 .
. 时,写出函数
时,写出函数 的单调递增区间;
的单调递增区间; 时,求函数
时,求函数 ,函数
,函数 在点
在点 处的切线方程为
处的切线方程为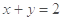 .
. ,
, 的值;
的值;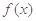 定义域内的任一个实数
定义域内的任一个实数 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. .
.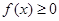 对一切
对一切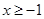 恒成立,求
恒成立,求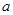 的取值范围;
的取值范围;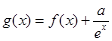 ,且
,且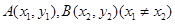 是曲线
是曲线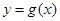 上任意两点,若对任意的
上任意两点,若对任意的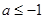 ,直线AB的斜率恒大于常数
,直线AB的斜率恒大于常数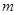 ,求
,求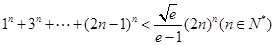 .
.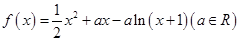 .
.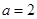 时,求函数
时,求函数 的极值;
的极值; ,使函数
,使函数 在
在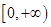 上有唯一的零点,若有,请求出
上有唯一的零点,若有,请求出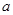 的范围;若没有,请说明理由.
的范围;若没有,请说明理由.