题目内容
已知向量 ,
, ,
, ,点A、B为函数
,点A、B为函数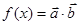 的相邻两个零点,AB=π.
的相邻两个零点,AB=π.
(1)求 的值;
的值;
(2)若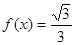 ,
,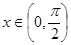 ,求
,求 的值;
的值;
(3)求 在区间
在区间 上的单调递减区间.
上的单调递减区间.
(1) ;(2)
;(2) ;(3)
;(3) ,
, .
.
解析试题分析: (1)由向量的数量积可得:
 .
.
这个函数相邻两个零点间的距离等于半个周期,再利用求周期的公式可得 的值.
的值.
(2)由(1)得 ,则
,则 .
.
这里不能展开来求 ,而应考虑凑角:
,而应考虑凑角:  ,这样再利用差角的正弦公式就可以求出
,这样再利用差角的正弦公式就可以求出 的值;
的值;
(3) ,这是一个三角函数与一个一次函数的差构成的函数,故可通过导数来求它的单调区间.
,这是一个三角函数与一个一次函数的差构成的函数,故可通过导数来求它的单调区间.
试题解析:(1)
 ,3分
,3分
由 ,得
,得 ,则
,则 .4分
.4分
(2)由(1)得 ,则
,则 .
.
由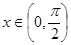 ,得
,得 ,6分
,6分


 .8分
.8分
(3) ,
, ,
,
∴ 10分
10分
∴ (
( ),
),
即 (
( ),
),
又 ,∴
,∴ 在区间
在区间 上的单调递减区间为:
上的单调递减区间为: ,
, . (12分)
. (12分)
考点:1、向量的数量积;2、三角函数的周期;3、三角变换;4、导数的应用.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 (万元),已知产品单价P(万元)与产品件数x满足:
(万元),已知产品单价P(万元)与产品件数x满足: ,生产100件这样的产品单价为50万元,产量定为多少件时总利润最大?
,生产100件这样的产品单价为50万元,产量定为多少件时总利润最大?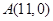 ,直线
,直线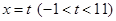 与函数
与函数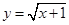 的图象交于点
的图象交于点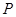 ,与
,与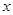 轴交于点
轴交于点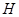 ,记
,记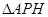 的面积为
的面积为 .
.
 在点
在点 处的切线方程为
处的切线方程为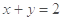 .
. ,
, 的值;
的值;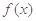 定义域内的任一个实数
定义域内的任一个实数 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. .
. 在
在 上是增函数,求正实数
上是增函数,求正实数 的取值范围;
的取值范围;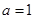 ,
, 且
且 ,设
,设 ,求函数
,求函数 在
在 上的最大值和最小值.
上的最大值和最小值. .
.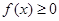 对一切
对一切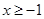 恒成立,求
恒成立,求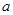 的取值范围;
的取值范围;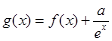 ,且
,且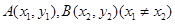 是曲线
是曲线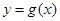 上任意两点,若对任意的
上任意两点,若对任意的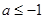 ,直线AB的斜率恒大于常数
,直线AB的斜率恒大于常数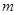 ,求
,求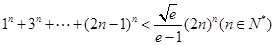 .
.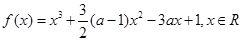 .
. 的单调区间;
的单调区间;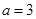 时,若函数
时,若函数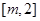 上的最大值为28,求
上的最大值为28,求 的取值范围.
的取值范围.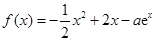 .
.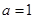 ,求
,求 在
在 处的切线方程;
处的切线方程; 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.