题目内容
已知函数 的一条对称轴为
的一条对称轴为 ,则φ值为
,则φ值为
- A.

- B.

- C.

- D.

D
分析:利用正弦函数的对称轴方程,求出函数的对称轴方程与 比较,选择k=1,即可求出φ值.
比较,选择k=1,即可求出φ值.
解答:由x+φ= (k∈Z).
(k∈Z).
解得对称轴方程为x= φ+kπ,(k∈Z).
φ+kπ,(k∈Z).
令 -φ+kπ,(k∈Z).
-φ+kπ,(k∈Z).
得φ= +kπ (k∈Z).
+kπ (k∈Z).
取k=1,φ= +π=
+π= .
.
故选D.
点评:本题考查正弦函数的对称轴方程的应用,考查计算能力.
分析:利用正弦函数的对称轴方程,求出函数的对称轴方程与
 比较,选择k=1,即可求出φ值.
比较,选择k=1,即可求出φ值.解答:由x+φ=
 (k∈Z).
(k∈Z).解得对称轴方程为x=
 φ+kπ,(k∈Z).
φ+kπ,(k∈Z).令
 -φ+kπ,(k∈Z).
-φ+kπ,(k∈Z).得φ=
 +kπ (k∈Z).
+kπ (k∈Z).取k=1,φ=
 +π=
+π= .
.故选D.
点评:本题考查正弦函数的对称轴方程的应用,考查计算能力.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
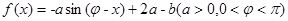 的一条对称轴为
的一条对称轴为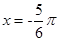 ,且
,且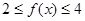
 的一条对称轴为
的一条对称轴为 ,则ω的最小值为 .
,则ω的最小值为 . 的一条对称轴为
的一条对称轴为 ,则φ值为( )
,则φ值为( )


