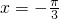题目内容
已知函数y=4cos(2x+φ)(|φ|<
)的图象经过点(0,2),则不是该函数的一条对称轴方程为( )
| π |
| 2 |
分析:由f(0)=4cosφ=2及|φ|<
可求φ,结合余弦函数在对称轴处取得函数的最值,结合选项可判断
| π |
| 2 |
解答:解:由题意可得f(0)=4cosφ=2
∴cosφ=
∵|φ|<
∴φ=±
,f(x)=4cos(2x±
π)
由于函数在对称轴处取得函数的最值,结合选项可知
当x=-
π时,2x±
π=-
π或
,不符合题意
故选C
∴cosφ=
| 1 |
| 2 |
∵|φ|<
| π |
| 2 |
∴φ=±
| π |
| 3 |
| 1 |
| 3 |
由于函数在对称轴处取得函数的最值,结合选项可知
当x=-
| 1 |
| 12 |
| 1 |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
故选C
点评:本题主要考查了余弦函数的性质:对称轴处取得函数的最值的应用,属于基础试题

练习册系列答案
相关题目
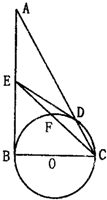 (选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点.
(选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点. 
 )的图象经过点(0,2),则不是该函数的一条对称轴方程为
)的图象经过点(0,2),则不是该函数的一条对称轴方程为