题目内容
在6道题中有4道理科题和2道文科题，如果不放回地依次抽取2道题，则在第1次抽到理科题的条件下，第2次抽到文科题的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：条件概率与独立事件
专题：应用题,概率与统计
分析：因为是不放回抽样，故在第1次抽到理科题的条件下，剩下2道文科题和3道理科题．根据随机事件的概率计算公式，不难算出第二次抽到文科题的概率．
解答：
解：因为是不放回的抽样，所以在第1次抽到理科题的条件下，剩下2道文科题和3道理科题
第二次抽取时，所有的基本事件有5个，符合“抽到理科题”的基本事件有2个
故在第1次抽到理科题的条件下，第2次抽到文科题的概率为：P=
故选：D．
第二次抽取时，所有的基本事件有5个，符合“抽到理科题”的基本事件有2个
故在第1次抽到理科题的条件下，第2次抽到文科题的概率为：P=
| 2 |
| 5 |
故选：D．
点评：本题给出无放回抽样模型，求在第1次抽到理科题的条件下，第2次抽到文科题的概率，着重考查了抽样方法的理解和随机事件的概率等知识，属于基础题．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
设全集U={1，2，3，4，5}，M={3，4}，N={2，3}，则图中阴影部分所表示的集合是（ ）
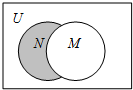
| A、{1，2，4} |
| B、{2，4} |
| C、{2} |
| D、{1，2，5} |
袋中共有6个除了颜色外完全相同的球，其中有1个红球，2个白球和3个黑球，从袋中任取1球，则取出的球为恰好是黑球的概率等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
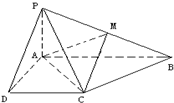已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=