题目内容
(2013•丽水一模)在△ABC中,角A,B,C所对的边分别为a,b,c,满足:ccosB+bcosC=4acosA.
(Ⅰ)求cosA的值;
(Ⅱ)若
•
=b+c,求△ABC的面积S的最小值.
(Ⅰ)求cosA的值;
(Ⅱ)若
| AB |
| AC |
分析:(Ⅰ)在△ABC中,利用正弦定理、两角和差的正弦、余弦公式,求得cosA的值.
(Ⅱ)根据条件,利用两个向量的数量积的定义和基本不等式,求得△ABC的面积S的最小值.
(Ⅱ)根据条件,利用两个向量的数量积的定义和基本不等式,求得△ABC的面积S的最小值.
解答:解:(Ⅰ)在△ABC中,由正弦定理得:sinCcosB+sinBcosC=4sinAcosAsin(B+C)=4sinAcosAsinA=4sinAcosA,
∵sinA≠0,∴cosA=
.…(6分)
(Ⅱ) 因为
•
=bccosA=
bc,所以,
bc=b+c≥2
bc≥64.
又 sinA=
,故S=
bcsinA≥
×64×
=8
,
当且仅当b=c时,Smin=8
.…(14分)
∵sinA≠0,∴cosA=
| 1 |
| 4 |
(Ⅱ) 因为
| AB |
| AC |
| 1 |
| 4 |
| 1 |
| 4 |
| bc |
又 sinA=
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| 15 |
当且仅当b=c时,Smin=8
| 15 |
点评:本题主要考查两个向量的数量积的运算,正弦定理,两角和差的正弦、余弦公式,基本不等式的应用,属于中档题.

练习册系列答案
相关题目
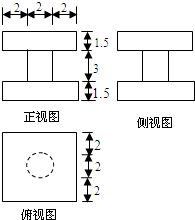 (2013•丽水一模)某几何体的三视图如图所示,则该几何体的体积为
(2013•丽水一模)某几何体的三视图如图所示,则该几何体的体积为 (2013•丽水一模)已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1),
(2013•丽水一模)已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1),