题目内容
（2013•丽水一模）若正数a，b满足2a+b=1，则4a2+b2+
的最大值为
．
| ab |
| 17 |
| 16 |
| 17 |
| 16 |
分析：由2a+b=1，a＞0，b＞0，利用基本不等式可求
的范围，令t=
，从而所求式子可转化为关于t的二次函数，结合二次函数的性质可求
| 2a•b |
| 2ab |
解答：解：∵2a+b=1，a＞0，b＞0
令t=
，则由基本不等式可得，
≤
=
即t∈(0，
]
则4a2+b2+
=(2a+b)2-4ab+
=1-4ab+
=1-2[（2a）b]+
=1-2t2+
=-2（t-
）2+
结合二次函数的性质可得，当t=
取得等号
故答案为：
令t=
| 2ab |
| 2ab |
| 2a+b |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则4a2+b2+
| ab |
| ab |
=1-4ab+
| ab |
| ||
|
=1-2t2+
| t | ||
|
=-2（t-
| ||
| 8 |
| 17 |
| 16 |
结合二次函数的性质可得，当t=
| ||
| 8 |
故答案为：
| 17 |
| 16 |
点评：本题主要考查了基本不等式及二次函数在求解最值中的应用，解题中要注意换元法的应用
练习册系列答案
名校课堂系列答案
相关题目
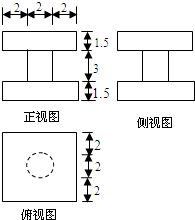（2013•丽水一模）某几何体的三视图如图所示，则该几何体的体积为
（2013•丽水一模）已知抛物线的顶点在坐标原点，焦点在y轴上，且过点（2，1），