题目内容
1.若二项式 ($\frac{2}{{\root{3}{x}}}$+$\sqrt{x}$)n的展开式中的常数项为第五项.求:(1)n的值;(2)设展开式中所有项系数和等于A,求$\root{10}{A}$的值;
(2)展开式中系数最大的项.
分析 (1)二项式 ($\frac{2}{{\root{3}{x}}}$+$\sqrt{x}$)n的展开式中的常数项为第五项.可得T5=${∁}_{n}^{4}$$(\frac{2}{\root{3}{x}})^{n-4}$$(\sqrt{x})^{4}$=2n-4${∁}_{n}^{4}$${x}^{2+\frac{4-n}{3}}$,令2+$\frac{4-n}{3}$=0,解得n.
(2)令x=1,则310=A,可得$\root{10}{A}$;
(3)Tr+1=${∁}_{10}^{r}$$(\frac{2}{\root{3}{x}})^{10-r}$$(\sqrt{x})^{r}$=${2}^{10-r}{∁}_{10}^{r}$${x}^{\frac{5r-10}{6}}$.令${2}^{10-r}{∁}_{10}^{r}$≥${2}^{11-r}{∁}_{10}^{r-1}$,${2}^{10-r}{∁}_{10}^{r}$≥${2}^{9-r}{∁}_{10}^{r+1}$,解得r即可得出.
解答 解:(1)∵二项式 ($\frac{2}{{\root{3}{x}}}$+$\sqrt{x}$)n的展开式中的常数项为第五项.∴T5=${∁}_{n}^{4}$$(\frac{2}{\root{3}{x}})^{n-4}$$(\sqrt{x})^{4}$=2n-4${∁}_{n}^{4}$${x}^{2+\frac{4-n}{3}}$,
令2+$\frac{4-n}{3}$=0,解得n=10.
(2)令x=1,则310=A,∴$\root{10}{A}$=3;
(3)Tr+1=${∁}_{10}^{r}$$(\frac{2}{\root{3}{x}})^{10-r}$$(\sqrt{x})^{r}$=${2}^{10-r}{∁}_{10}^{r}$${x}^{\frac{5r-10}{6}}$.
令${2}^{10-r}{∁}_{10}^{r}$≥${2}^{11-r}{∁}_{10}^{r-1}$,${2}^{10-r}{∁}_{10}^{r}$≥${2}^{9-r}{∁}_{10}^{r+1}$,
解得r=4.
∴展开式中系数最大的项是T5=${2}^{4}{∁}_{10}^{4}$${x}^{\frac{5}{3}}$.
点评 本题考查了二项式定理的通项公式性质及其应用,考查了推理能力与计算能力,属于中档题.

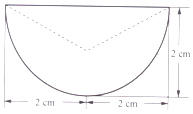 某零件的正视图与侧视图均是如图所示的图形(实线组成半径为2cm的半圆,虚线是底边上高为1cm的等腰三角形的两腰),俯视图是一个半径为2cm的圆(包括圆心),则该零件的体积是( )
某零件的正视图与侧视图均是如图所示的图形(实线组成半径为2cm的半圆,虚线是底边上高为1cm的等腰三角形的两腰),俯视图是一个半径为2cm的圆(包括圆心),则该零件的体积是( )| A. | $\frac{4}{3}πc{m^3}$ | B. | $\frac{8}{3}πc{m^3}$ | C. | 4πcm3 | D. | $\frac{20}{3}πc{m^3}$ |