题目内容
如图,点P在⊙O的直径AB的延长线上,PQ切⊙O于Q,连结AQ、BQ,∠APQ的平分线分别交QA、QB于M、N.求证:MN2=2AM·BN.
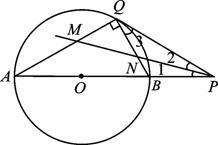
证明:∵PQ是切线,∴∠3=∠A.又∠1=∠2,∴∠QMN=∠QNM.∴QM=QN.
又AB是直径,∴MN=2QM.
∵∠1=∠2,
∴![]() , ①
, ①
![]() . ②
. ②
①×②得![]() =1(QP2=PB·PA),
=1(QP2=PB·PA),
∴QM2=BN·AM.又MN=2QM,
∴MN2=2BN·AM.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数
如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数

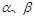 的交线, 已知二面角
的交线, 已知二面角 为直二面角,
为直二面角, 
 , ∠BAP=45°.
, ∠BAP=45°. 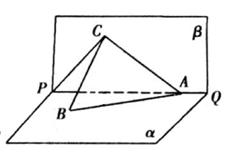
 内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心?
内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心? 时, 求二面角B-AC-P的大小.
时, 求二面角B-AC-P的大小.
