题目内容
10.设Sn是数列{an}的前n项和,n≥2时点(an-1,2an)在直线y=2x+1上,且{an}的首项a1是二次函数y=x2-2x+3的最小值,则S9=36.分析 由题意可得${a_n}-{a_{n-1}}=\frac{1}{2}$(n≥2),再由配方法求出二次函数y=x2-2x+3的最小值得a1,代入等差数列的前n项和得答案.
解答 解:∵(an-1,2an)在直线y=2x+1上,
∴2an=2an-1+1,即${a_n}-{a_{n-1}}=\frac{1}{2}$(n≥2),
又y=x2-2x+3=(x-1)2+2,∴a1=2,
则S9=$9×2+\frac{9×8}{2}×\frac{1}{2}=36$.
故答案为:36.
点评 本题考查等差数列的通项公式,考查等差数列的前n项和,是基础的计算题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
5.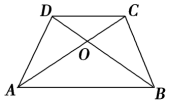 如图所示,梯形ABCD的对角线交于点O,则下列四个结论:
如图所示,梯形ABCD的对角线交于点O,则下列四个结论:
①△AOB∽△COD;
②△AOD∽△ACB;
③S△DOC:S△AOD=CD:AB;
④S△AOD=S△BOC.
其中正确的个数为( )
 如图所示,梯形ABCD的对角线交于点O,则下列四个结论:
如图所示,梯形ABCD的对角线交于点O,则下列四个结论:①△AOB∽△COD;
②△AOD∽△ACB;
③S△DOC:S△AOD=CD:AB;
④S△AOD=S△BOC.
其中正确的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.已知△ABC的顶点A(0,-4)、B(0,4),且4(sinB-sinA)=3sinC,则顶点C的轨迹方程是( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{7}$=1(x>3) | B. | $\frac{{x}^{2}}{7}$-$\frac{{y}^{2}}{9}$=1(x<-7) | C. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{7}$=1(y>3) | D. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{7}$=1(y<-3) |
19.已知实数x,y满足约束条件$\left\{\begin{array}{l}x≥0\\ x-y≤0\\ x+y≤a\end{array}\right.({a>0})$,若z=x+ay的最大值为2,则$m+\frac{a^2}{{m-\sqrt{2}}}({m>\sqrt{2}})$的最小值为( )
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | 6 |