题目内容
(10分)设函数 .
.
⑴ 求 的极值点;
的极值点;
⑵ 若关于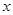 的方程
的方程 有3个不同实根,求实数a的取值范围.
有3个不同实根,求实数a的取值范围.
⑶ 已知当 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
 .
.⑴ 求
 的极值点;
的极值点;⑵ 若关于
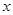 的方程
的方程 有3个不同实根,求实数a的取值范围.
有3个不同实根,求实数a的取值范围.⑶ 已知当
 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围. ⑴ ;⑵
;⑵ ;(3)
;(3) 。
。
 ;⑵
;⑵ ;(3)
;(3) 。
。试题分析:⑴
 .
.⑵ 由(Ⅰ)的分析可知
 图象的大致形状及走向(图略)
图象的大致形状及走向(图略)∴当
 的图象有3个不同交点,
的图象有3个不同交点,即方程
 有三解
有三解⑶

∵
 上恒成立
上恒成立令
 ,由二次函数的性质,
,由二次函数的性质, 上是增函数,
上是增函数,∴
 ∴所求k的取值范围是
∴所求k的取值范围是 .
.点评:解决恒成立问题常用变量分离法,变量分离法主要通过两个基本思想解决恒成立问题, 思路1:
 在
在 上恒成立
上恒成立 ;思路2:
;思路2:  在
在 上恒成立
上恒成立 。注意恒成立问题与存在性问题的区别。
。注意恒成立问题与存在性问题的区别。
练习册系列答案
相关题目
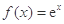 (
( 为自然对数的底数),
为自然对数的底数), (
( ).
).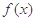
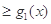 ;
;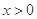 时,比较
时,比较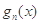 的大小,并说明理由;
的大小,并说明理由;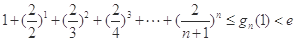 (
(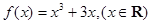 ,当
,当 时,
时,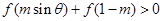 恒成立,则实数
恒成立,则实数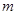 的取值范围是
的取值范围是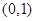
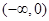
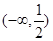
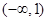
 时,
时, 且
且 ,则不等式
,则不等式 的解集是( )
的解集是( )



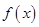 的导数为
的导数为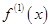 ,
,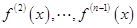 的导数为
的导数为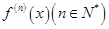 。若
。若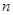 次求导,则
次求导,则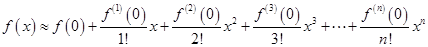
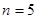 ,根据这个结论,则可近似估计自然对数的底数
,根据这个结论,则可近似估计自然对数的底数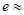 _____(用分数表示).
_____(用分数表示).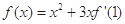 ,则
,则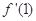 为
为 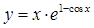 的导数为 。
的导数为 。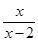 在点(1,-1)处的切线方程为
在点(1,-1)处的切线方程为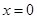 是函数
是函数 的一个极值点,且函数
的一个极值点,且函数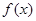 的图象在
的图象在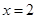 处的切线的斜率为2
处的切线的斜率为2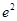 .
.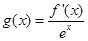 ,其中
,其中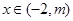 ,问:对于任意的
,问:对于任意的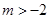 ,方程
,方程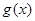
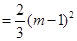 在区间
在区间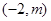 上是否存在实数根?若存在,请确定实数根的个数.若不存在,请说明理由.(9分)
上是否存在实数根?若存在,请确定实数根的个数.若不存在,请说明理由.(9分)