题目内容
7.已知函数f(x)=Asin(ωx+φ)+B( A>0,ω>0,$|φ|<\frac{π}{2}$,x∈R),在同一个周期内,当$x=\frac{π}{4}$时,函数取最大值3,当$x=\frac{7π}{12}$时,函数取最小值-1,(1)求函数f(x)的解析式;
(2)将f(x)的图象上所有点向左平移$\frac{π}{6}$个单位,再将所得图象上所有点的横坐标变为原来的$\frac{3}{2}$倍,得到g(x)的图象,讨论g(x)在$[{-\frac{π}{2},\frac{π}{2}}]$上的单调性.
分析 (1)根据最值计算A,B,根据周期计算ω,根据f($\frac{π}{4}$)=3计算φ;
(2)根据函数图象变换得出g(x)的解析式,求出g(x)的单调区间即可.
解答 解:(1)由题意得$\left\{\begin{array}{l}{A+B=3}\\{-A+B=-1}\end{array}\right.$,∴$\left\{\begin{array}{l}{A=2}\\{B=1}\end{array}\right.$.
f(x)的周期T=2($\frac{7π}{12}-\frac{π}{4}$)=$\frac{2π}{3}$.
∴$\frac{2π}{ω}$=$\frac{2π}{3}$,即ω=3.
∵f($\frac{π}{4}$)=2sin($\frac{3π}{4}$+φ)+1=3,
∴$\frac{3π}{4}$+φ=$\frac{π}{2}$+2kπ,∴φ=-$\frac{π}{4}$+2kπ,k∈Z,
∵|φ|<$\frac{π}{2}$,∴φ=-$\frac{π}{4}$.
∴f(x)=2sin(3x-$\frac{π}{4}$)+1.
(2)g(x)=2sin(2x+$\frac{π}{4}$)+1,
令-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{4}$≤$\frac{π}{2}$+2kπ,解得-$\frac{3π}{8}$+kπ≤x≤$\frac{π}{8}$+kπ,k∈Z.
[-$\frac{3π}{8}$+kπ,$\frac{π}{8}$+kπ]∩[-$\frac{π}{2}$,$\frac{π}{2}$]=[-$\frac{3}{8}$π,$\frac{π}{8}$],
∴g(x)在[-$\frac{3}{8}$π,$\frac{π}{8}$]上单调递增,在[-$\frac{π}{2}$,-$\frac{3π}{8}$],[$\frac{π}{8}$,$\frac{π}{2}$]上单调递减.
点评 本题考查了三角函数的图象与性质,函数图象变换,属于中档题.

| A. | x=8 | B. | x=-8 | C. | x=-16 | D. | x=16 |
| A. | x+y+3=0 | B. | x-y+3=0 | C. | x+y-3=0 | D. | x+y-5=0 |
| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $2\sqrt{3}$ | C. | 6 | D. | $4\sqrt{3}$ |
 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.求二面角P-BC-D余弦值的大小.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.求二面角P-BC-D余弦值的大小. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,动点P在其表面上运动,且|PA|=x,把点的轨迹长度L=f(x)称为“喇叭花”函数,给出下列结论:
如图,在棱长为1的正方体ABCD-A1B1C1D1中,动点P在其表面上运动,且|PA|=x,把点的轨迹长度L=f(x)称为“喇叭花”函数,给出下列结论: 的图象,可将函数
的图象,可将函数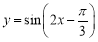 的图象( )
的图象( ) 个单位 B.向左平移
个单位 B.向左平移 个单位
个单位 个单位 D.向右平移
个单位 D.向右平移 个单位
个单位