题目内容
3.求适合下列条件的圆锥曲线的标准方程.(1)与椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1有公共焦点,且离心率为2的双曲线;
(2)中心在坐标原点,经过点A(2,3),且点F(2,0)为其右焦点的椭圆.
分析 (1)设双曲线的标准方程为:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0).椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的焦点(±4,0),$\frac{c}{a}$=2,c2=a2+b2,联立解得即可得出.
(2)依题意,可设椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),则$\left\{\begin{array}{l}{\frac{4}{{a}^{2}}+\frac{9}{{b}^{2}}=1}\\{{a}^{2}-{b}^{2}=4}\end{array}\right.$,解出即可得出.
解答 解:(1)设双曲线的标准方程为:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0).
椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的焦点(±4,0),$\frac{c}{a}$=2,c2=a2+b2,联立解得a=2,b=2$\sqrt{3}$.
即所求双曲线的方程$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}$=1.
(2)依题意,可设椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
则$\left\{\begin{array}{l}{\frac{4}{{a}^{2}}+\frac{9}{{b}^{2}}=1}\\{{a}^{2}-{b}^{2}=4}\end{array}\right.$,
解得b2=12,a2=16,
所以椭圆C的方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}$=1.
点评 本题考查了椭圆与双曲线的定义标准方程及其性质,考查了推理能力与计算能力,属于中档题.

 发散思维新课堂系列答案
发散思维新课堂系列答案| A. | $(0,\frac{1}{4})$ | B. | $(\frac{1}{4},1)$ | C. | (1,4) | D. | (4,+∞) |
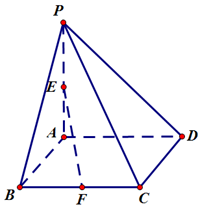 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为矩形,F是BC的中点,且PA=BC=2AB=2.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为矩形,F是BC的中点,且PA=BC=2AB=2.