题目内容
13.已知函数f(x)=logax+x-3(a>0且a≠1)有两个零点x1,x2,且x1<x2,若x2∈(3,4),则实数a的取值范围是( )| A. | $(0,\frac{1}{4})$ | B. | $(\frac{1}{4},1)$ | C. | (1,4) | D. | (4,+∞) |
分析 函数f(x)有两个不同的零点,可转化为函数y=logax与y=3-x的图象有两个交点,在同一坐标系中,分别作出这两个函数的图象,观察图象,可得答案.
解答 解:若函数f(x)有两个不同的零点,
则函数y=logax与y=3-x的图象有两个交点,
在同一坐标系中,分别作出这两个函数的图象,如下图所示: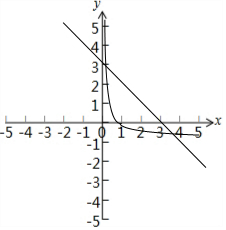
观察图象,可知若使二者有两个交点,须使0<a<1;
而若使x2∈(3,4),又须使$\left\{{\begin{array}{l}{{{log}_a}3<0}\\{{{log}_a}4>-1}\end{array}}\right.$
解得$0<a<\frac{1}{4}$.
故选:A
点评 本题主要考查了函数的零点和图象的交点的关系,以及对数函数的性质,难度中档.

练习册系列答案
相关题目
4.在等差数列{an}中,已知a3+a9=16,则a5+a7=( )
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
8.函数$f(x)={2^{\frac{1}{x}}}(\frac{1}{2}≤x≤1)$的值域是( )
| A. | $[\frac{1}{2},\frac{{\sqrt{2}}}{2}]$ | B. | $[\frac{{\sqrt{2}}}{2},2]$ | C. | (0,2] | D. | [2,4] |
18.2016年11月21日是附中建校76周年校庆日,为了了解在校同学们对附中的看法,学校进行了调查,从全校所有班级中任选三个班,统计同学们对附中的看法,情况如下表:
(1)从这三个班中各选一位同学,求恰好有2人认为附中“非常好”的概率(用比例作为相应概率);
(2)若在B班按所持态度分层抽样,抽取9人,再从这9人中任意选取3人,记认为附中“非常好”的人数为ξ,求ξ的分布列和数学期望.
| 对附中的看法 | 非常好,附中推行素质教育,身心得以全面发展 | 很好,我的高中生活很快乐很充实 |
| A班人数比例 | $\frac{3}{4}$ | $\frac{1}{4}$ |
| B班人数比例 | $\frac{2}{3}$ | $\frac{1}{3}$ |
| C班人数比例 | $\frac{1}{2}$ | $\frac{1}{2}$ |
(2)若在B班按所持态度分层抽样,抽取9人,再从这9人中任意选取3人,记认为附中“非常好”的人数为ξ,求ξ的分布列和数学期望.
3.设a,b,c为互不相等的正数,则下列不等式不一定成立的是( )
| A. | |a-b|≤|a|+|b| | B. | |a-b|≤|a-c|+|b-c| | C. | $\frac{b}{a}$<$\frac{b+c}{a+c}$ | D. | a2+$\frac{1}{{a}^{2}}$≥a+$\frac{1}{a}$ |