题目内容
14.${∫}_{0}^{1}$$\sqrt{1-{x}^{2}}$dx+${∫}_{1}^{2}$$\frac{1}{x}$dx=$\frac{π}{4}$+ln2.分析 分别利用定积分的几何意义以及找出原函数的方法求定积分即可.
解答 解:原式=$\frac{1}{4}π×{1}^{2}+lnx{|}_{1}^{2}$=$\frac{π}{4}+ln2$;
故答案为:$\frac{π}{4}$+ln2;
点评 本题考查了定积分的计算;分别利用了定积分的几何意义以及找出原函数求定积分的值.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
2.关于x的方程(m+3)x2-4mx+2m-1=0的两根异号,且负根的绝对值比正根大,那么实数m的取值范围为( )
| A. | (-3,0) | B. | (0,3) | C. | (-∞,-3)∪(0,+∞) | D. | (-∞,0)∪(3,+∞) |
9.在等腰梯形ABCD中,AB=2CD=2,∠DAB=60°,E是AB的中点,将△ADE与△BEC分别沿ED,EC向上折起,使A,B重合于点P,若三棱锥P-CDE的各个顶点在同一球面上,则该球的表面积为( )
| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{\sqrt{6}π}{2}$ | C. | $\frac{\sqrt{6}π}{8}$ | D. | $\frac{3π}{2}$ |
19.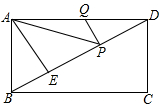 如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P,Q分别在BD,AD上,
如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P,Q分别在BD,AD上,
则AP+PQ的最小值为( )
 如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P,Q分别在BD,AD上,
如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P,Q分别在BD,AD上,则AP+PQ的最小值为( )
| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $3\sqrt{3}$ |
4.在等差数列{an}中,已知a3+a9=16,则a5+a7=( )
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{\sqrt{2}}{2}$AD
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{\sqrt{2}}{2}$AD