题目内容
15.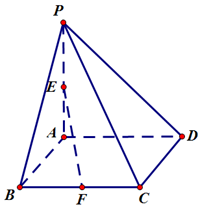 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为矩形,F是BC的中点,且PA=BC=2AB=2.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为矩形,F是BC的中点,且PA=BC=2AB=2.(1)求证:CD⊥PA
(2)线段PA是否存在一点E,使得EF∥平面PCD?若有,请找出具体位置,并加以证明,若无,请分析说明理由.
分析 (1)根据PA⊥底面ABCD可以推知CD⊥PA;
(2)当E是PA的中点时,EF∥平面PCD.如图,取PD的中点G,连接EG、CG,构建平行四边形EFCG,结合平行四边形的对边相互平行的性质和线面平行的性质证得结论EF∥平面PCD.
解答  证明:(1)又因为PA⊥底面ABCD,
证明:(1)又因为PA⊥底面ABCD,
CD?底面ABCD,所以CD⊥PA;
解:(2)当E是PA的中点时,EF∥平面PCD,
取PD的中点G,连接EG、CG,
又因为E、F分别是PA、BC的中点,底面ABCD为矩形,
所以EG∥AD∥FC且EG∥$\frac{1}{2}$AD∥FC,
所以四边形EFCG是平行四边形,
所以EF∥GC.
又因为EF?平面PCD,GC?平面PCD,
所以EF∥平面PCD.
点评 本题以底面为长方形、一条侧棱垂直于底的四棱锥为载体,通过证明线面平行、垂直,着重考查了线面平行的判定定理、线面垂直的判定与性质等知识点,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.平面向量$\overrightarrow{a}$,$\overrightarrow{b}$共线的充要条件是( )
| A. | $\overrightarrow{a}$,$\overrightarrow{b}$方向相同 | |
| B. | $\overrightarrow{a}$,$\overrightarrow{b}$两向量中至少有一个为零向量 | |
| C. | ?λ∈R,$\overrightarrow{b}$=λ$\overrightarrow{a}$ | |
| D. | 存在不全为零的实数λ1,λ2,λ1$\overrightarrow{a}$+λ2$\overrightarrow{b}$=$\overrightarrow{0}$ |
4.在等差数列{an}中,已知a3+a9=16,则a5+a7=( )
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{\sqrt{2}}{2}$AD
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{\sqrt{2}}{2}$AD