题目内容
已知空间向量
=(-
,
,-
),
=(-
,-
,-
),则
和
的夹角为( )
| a |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
| b |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| a |
| b |
| A、60° | B、120° |
| C、90° | D、30° |
考点:空间向量的数量积运算
专题:空间向量及应用
分析:由已知条件利用cos<
,
>=
,能求出
和
的夹角.
| a |
| b |
| ||||
|
|
| a |
| b |
解答:
解:∵
=(-
,
,-
),
=(-
,-
,-
),
∴cos<
,
>=
=
=
,
∴
和
的夹角为60°.
故选:A.
| a |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
| b |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
∴cos<
| a |
| b |
| ||||
|
|
=
| ||||||||
|
| 1 |
| 2 |
∴
| a |
| b |
故选:A.
点评:本题考查空间中两个向量的夹角的求法,是基础题,解题时要注意cos<
,
>=
的合理运用.
| a |
| b |
| ||||
|
|

练习册系列答案
相关题目
关于平面向量
、
、
,有下列四种说法:
①若
≠0,
•
=0,则
=0;
②若
≠0,
•
=
•
,则
=
;
③对任意向量
、
、
,有(
•
)•
=
•(
•
);
④若
∥
,
∥
,则
∥
,
其中正确的个数是( )
| a |
| b |
| c |
①若
| a |
| a |
| b |
| b |
②若
| a |
| a |
| b |
| a |
| c |
| b |
| c |
③对任意向量
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
④若
| a |
| b |
| b |
| c |
| a |
| c |
其中正确的个数是( )
| A、0 | B、1 | C、2 | D、3 |
函数y=3x-8+log2x的零点一定位于的区间为( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
若{2,3}?M?{1,2,3,4,5},则M的个数为( )
| A、5 | B、6 | C、7 | D、8 |
函数f(x)=2sinωx(ω>0)在区间[0,
]上单调递增,且在这个区间上的最大值是
,那么ω=( )
| π |
| 4 |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |
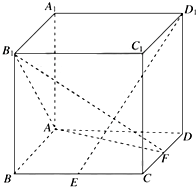 如图,正方体ABCD-A1B1C1D1中,E是棱BC的中点,点F是棱CD上的动点.
如图,正方体ABCD-A1B1C1D1中,E是棱BC的中点,点F是棱CD上的动点.