题目内容
14．
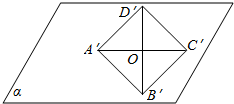在水平放置的平面α内有一个边长为1的正方形A′B′C′D′．如图，其中的对角线A′C′在水平位置，已知该正方形是某个四边形用斜二测画法画出的直观图，试画出该四边形的真实图形并求出其面积．
分析 设正方形A′B′C′D′是四边形ABCD的直观图，根据斜二测画法可得到原图，进而得到面积．
解答 解：设正方形A′B′C′D′是四边形ABCD的直观图，
则四边形ABCD是平行四边形，且AD=2，对角线AC=$\sqrt{2}$，原图如下所示：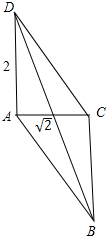
其面积S=2×$\frac{1}{2}$×$2×\sqrt{2}$=2$\sqrt{2}$．
点评 本题考查的知识点是平面图形的直观图，熟练掌握斜二测画法是解答的关键，难度不大，属于基础题．
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目