题目内容
6.已知集合A={x|x2+2x+a=0},集合B={x|x=-1}.(1)若A?B,求a的取值范围;
(2)若A⊆B,求a的取值范围;
(3)若B⊆A,求a的值.
分析 (1)若A?B,则A只能为空集,△=4-4a<0;
(2)若A⊆B,则A为空集或含有一个元素,△=4-4a≤0;
(3)若B⊆A,则1-2+a=0,即可求a的值.
解答 解:(1)若A?B,则A只能为空集,∴△=4-4a<0,∴a>1;
(2)若A⊆B,则A为空集或含有一个元素,∴△=4-4a≤0,∴a≥1;
(3)若B⊆A,则1-2+a=0,∴a=1.
点评 本题考查集合的包含关系,考查判别式的运用,正确理解题意是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知sin(π-α)=-$\frac{\sqrt{10}}{10}$,则$\frac{2si{n}^{2}α+sin2α}{cos(α-\frac{π}{4})}$=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{2\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | 2 |
18.设g(x)=2x+3,g(x+2)=f(x),则f(x)等于( )
| A. | -2x+1 | B. | 2x-1 | C. | 2x-3 | D. | 2x+7 |
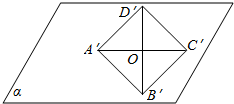 在水平放置的平面α内有一个边长为1的正方形A′B′C′D′.如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.
在水平放置的平面α内有一个边长为1的正方形A′B′C′D′.如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.