题目内容
5.已知动点C与两定点A(0,0),B(3,0)的距离的比为$\frac{1}{2}$,则△ABC面积的最大值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 利用动点C与两定点A(0,0),B(3,0)的距离的比为$\frac{1}{2}$,确定C的轨迹方程,求出圆上点C到直线AB距离的最大值为5,即可求出△ABC的面积的最大值.
解答 解:设C(x,y),则
∵动点C与两定点A(0,0),B(3,0)的距离的比为$\frac{1}{2}$,∴(x-0)2+(y-0)2=$\frac{1}{4}$[(x-3)2+(y-0)2,
即x2+y2+2x=3,即(x+1)2+y2=4
∴圆上点C到直线AB距离的最大值为2,
∴△ABC的面积的最大值为$\frac{1}{2}$×2×3=3,
故选:B.
点评 本题考查轨迹方程,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
13.函数y=log2(x2+2x-3)的单调递减区间为( )
| A. | (-∞,-3) | B. | (-∞,-1) | C. | (1,+∞) | D. | (-3,-1) |
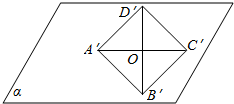 在水平放置的平面α内有一个边长为1的正方形A′B′C′D′.如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.
在水平放置的平面α内有一个边长为1的正方形A′B′C′D′.如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.