题目内容
4.函数f(x)=sin($\frac{4}{3}$x-sinx)在[0,π]上的值域为[-$\frac{\sqrt{3}}{2}$,1].分析 令t=$\frac{4}{3}$x-sinx,利用单调性求函数t的值域,再利用正弦函数的定义域和值域求得f(x)=sint 的值域.
解答 解:令t=$\frac{4}{3}$x-sinx,由于t′=$\frac{4}{3}$-cosx在[0,π]上的大于零,故函数t在[0,π]上单调递增,
故t∈[0,$\frac{4π}{3}$],故函数f(x)=sin($\frac{4}{3}$x-sinx)=sint 的值域为[-$\frac{\sqrt{3}}{2}$,1],
故答案为:[-$\frac{\sqrt{3}}{2}$,1].
点评 本题主要考查利用导数研究函数的单调性,利用单调性求函数的值域,正弦函数的定义域和值域,属于中档题.

练习册系列答案
相关题目
14.甲、乙两名同学参加某种选拔测试,在相同测试条件下,两人5次此时的成绩(单位:分)如下表:
(Ⅰ)请计算甲、乙两人成绩的平均数和方差,并据此判断选派谁参赛更好?
(Ⅱ)若从甲、乙两人所有成绩大于70分的数据中,随机各抽取一个成绩进行比较,求甲成绩比乙成绩好的概率.
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 甲 | 59 | 62 | 76 | 80 | 88 |
| 乙 | 56 | 66 | 76 | 78 | 89 |
(Ⅱ)若从甲、乙两人所有成绩大于70分的数据中,随机各抽取一个成绩进行比较,求甲成绩比乙成绩好的概率.
12.函数f(x)=loga(2-ax2)在(0,1)上为减函数,则实数a的取值范围是( )
| A. | [$\frac{1}{2}$,1) | B. | (1,2) | C. | (1,2] | D. | ($\frac{1}{2}$,1) |
13.函数y=log2(x2+2x-3)的单调递减区间为( )
| A. | (-∞,-3) | B. | (-∞,-1) | C. | (1,+∞) | D. | (-3,-1) |
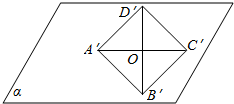 在水平放置的平面α内有一个边长为1的正方形A′B′C′D′.如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.
在水平放置的平面α内有一个边长为1的正方形A′B′C′D′.如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.