题目内容
14.求圆心在直线4x+y=0上,且与直线l:x+y-1=0切于点P(3,-2)的圆的方程,并找出圆的圆心及半径.分析 设圆的方程为(x-a)2+(y-b)2=r2(r>0),由圆心在直线y=-4x上,并且与直线l:x+y-1=0相切于点P(3,-2),可以构造a,b,r的方程组,解方程组可得a,b,r的值,进而得到圆的方程.
解答 解:设圆的方程为(x-a)2+(y-b)2=r2(r>0)
由题意有:$\left\{\begin{array}{l}{b=-4a}\\{\frac{|a+b-1|}{\sqrt{2}}=r}\\{\frac{b+2}{a-3}•(-1)=-1}\end{array}\right.$
解之得a=1,b=-4,r=2$\sqrt{2}$.
∴所求圆的方程为(x-1)2+(y+4)2=8,圆心坐标为(1,-4),半径为2$\sqrt{2}$.
点评 本题考查的知识点是直线与圆的位置关系,圆的标准方程,其中根据已知构造关于圆心坐标及半径的方程组,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知A(1,0)、B(2,-1),若点P(x,y)满足x+y+1=0,则|PA|+|PB|的最小值为( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{10}$ | D. | $\sqrt{13}$ |
5.对于两个平面α,β和两条直线m,n,下列命题中真命题是( )
| A. | 若m⊥α,m⊥n,则n∥α | B. | 若m∥α,α⊥β,则m⊥β | ||
| C. | 若m∥α,n∥β,α⊥β,则m⊥n | D. | 若m⊥α,n⊥β,α⊥β,则m⊥n |
19.某酒店将顾客的2辆不同的奔驰轿车、1辆现代轿车、3辆不同高尔夫轿车停放在一排6个车位上,则2辆奔驰轿车相邻且奔驰轿车与现代轿车不相邻的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
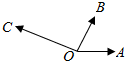 如图所示,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}$⊥$\overrightarrow{OC}$.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别是( )
如图所示,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}$⊥$\overrightarrow{OC}$.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别是( )