题目内容
16．（x2+x+1）（1-x）6展开式中x2的系数为10．分析 （x2+x+1）（1-x）6=（x2+x+1）（1-6x+${∁}_{6}^{2}{x}^{2}$+…）即可得出．
解答 解：（x2+x+1）（1-x）6=（x2+x+1）（1-6x+${∁}_{6}^{2}{x}^{2}$+…）
展开式中x2的系数为1-6+${∁}_{6}^{2}$=10．
故答案为：10．
点评 本题考查了二项式定理的应用，考查了推理能力与计算能力，属于基础题．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
11．小明同学在寒假社会实践活动中，对白天平均气温与某家奶茶店的A品牌饮料销量之间的关系进行了分析研究，他分别记录了1月11日至1月15日的白天气温x（°C）与该奶茶店的A品牌饮料销量y（杯），得到如下表数据：
（Ⅰ）若先从这五组数据中抽出2组，求抽出的2组书记恰好是相邻2天数据的概率；
（Ⅱ）请根据所给五组书记，求出y关于x的线性回归方程式$\widehaty=\widehatbx+\widehata$．
（Ⅲ）根据（Ⅱ）所得的线性回归方程，若天气预报1月16号的白天平均气温为7（℃），请预测该奶茶店这种饮料的销量．
（参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n（\overline{x}）^{2}}$，$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x）
| 日期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
| 平均气温x（℃） | 9 | 10 | 12 | 11 | 8 |
| 销量y（杯） | 23 | 25 | 30 | 26 | 21 |
（Ⅱ）请根据所给五组书记，求出y关于x的线性回归方程式$\widehaty=\widehatbx+\widehata$．
（Ⅲ）根据（Ⅱ）所得的线性回归方程，若天气预报1月16号的白天平均气温为7（℃），请预测该奶茶店这种饮料的销量．
（参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n（\overline{x}）^{2}}$，$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x）
1．已知点M在角θ终边的延长线上，且|OM|=2，则M的坐标为（ ）
| A． | （2cosθ，2sinθ） | B． | （-2cosθ，2sinθ） | C． | （-2cosθ，-2sinθ） | D． | （2cosθ，-2sinθ） |
8．在△ABC中，若sinA：sinB：sinC=2：3：4，则最大角的余弦值为（ ）
| A． | $\frac{1}{3}$ | B． | $-\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $-\frac{1}{4}$ |
5．
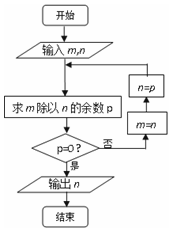执行右面的程序框图，如果输入m=72，n=30，则输出的n是（ ）
执行右面的程序框图，如果输入m=72，n=30，则输出的n是（ ）| A． | 12 | B． | 6 | C． | 3 | D． | 0 |