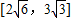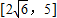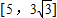题目内容
若关于x的方程asinx•cosx+sin2x-3=0在x∈[
，
]恒有解，则实数a的取值范围是（ ）
| π |
| 4 |
| π |
| 3 |
分析：通过化简方程为a的表达式，利用x的范围，通过基本不等式以及函数的单调性求出函数的最值，求出a的取值范围．
解答：解：关于x的方程asinx•cosx+sin2x-3=0，
化为a=
=2tanx+
，因为x∈[
，
]，
所以a≥2
=2
，当且仅当tanx=
时a取得最小值，
当x=
时，a=3
，x=
时，a=5，又3
＞5，
所以a∈[2
，3
]，此时方程在x∈[
，
]时方程恒有解．
故选 A．
化为a=
| 3-sin2x |
| sinxcosx |
| 3 |
| tanx |
| π |
| 4 |
| π |
| 3 |
所以a≥2
2tanx•
|
| 6 |
3
| ||
| 2 |
当x=
| π |
| 3 |
| 3 |
| π |
| 4 |
| 3 |
所以a∈[2
| 6 |
| 3 |
| π |
| 4 |
| π |
| 3 |
故选 A．
点评：本题考查函数与方程的综合应用，函数的最值的求法，转化思想的应用，考查分析问题解决问题的能力．
练习册系列答案
阅读快车系列答案
相关题目
恒有解，则实数a的取值范围是
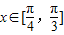恒有解，则实数a的取值范围是（ ）
