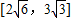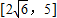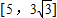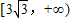题目内容
若关于x的方程asinx•cosx+sin2x-3=0在x∈[
，
]恒有解，则实数a的取值范围是（ ）
| π |
| 4 |
| π |
| 3 |
A．[2
| B．[2
| C．[5，3
| D．[3
|
关于x的方程asinx•cosx+sin2x-3=0，
化为a=
=2tanx+
，因为x∈[
，
]，
所以a≥2
=2
，当且仅当tanx=
时a取得最小值，
当x=
时，a=3
，x=
时，a=5，又3
＞5，
所以a∈[2
，3
]，此时方程在x∈[
，
]时方程恒有解．
故选 A．
化为a=
| 3-sin2x |
| sinxcosx |
| 3 |
| tanx |
| π |
| 4 |
| π |
| 3 |
所以a≥2
2tanx•
|
| 6 |
3
| ||
| 2 |
当x=
| π |
| 3 |
| 3 |
| π |
| 4 |
| 3 |
所以a∈[2
| 6 |
| 3 |
| π |
| 4 |
| π |
| 3 |
故选 A．
练习册系列答案
相关题目
恒有解，则实数a的取值范围是
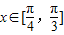恒有解，则实数a的取值范围是（ ）
