Question

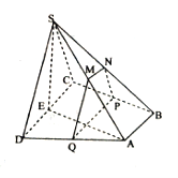
【题目】如图，四棱锥的底面是边长为1的正方形，侧棱底面，且， 是侧棱上的动点．

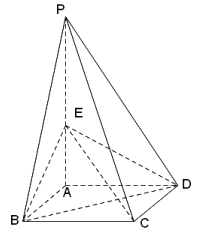
（Ⅰ）求四棱锥的体积；

（Ⅱ）如果是的中点，求证平面；

（Ⅲ）是否不论点在侧棱的任何位置，都有？证明你的结论．

Answer 1

【答案】（Ⅰ）;（Ⅱ）见解析;（Ⅲ）不论点在何位置，都有．

【解析】试题分析：（Ⅰ） 平面知棱锥得高即为，所以根据体积公式得： ．（Ⅱ）连结交于，连结．

根据中位线知，由线面平行的判定定理知平面．（Ⅲ）不论点在何位置，都有．由题意易知平面．所以不论点在何位置，都有平面，故都有．

试题解析：（Ⅰ）∵平面，

∴，

即四棱锥的体积为．

（Ⅱ）连结交于，连结．

∵四边形是正方形，∴是的中点，

又∵是的中点，∴，

∵平面， 平面，

∴平面．

（Ⅲ）不论点在何位置，都有．

证明如下：∵四边形是正方形，∴，

∵底面，且平面，∴，

又∵，∴平面．

∵不论点在何位置，都有平面，

∴不论点在何位置，都有．