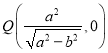题目内容
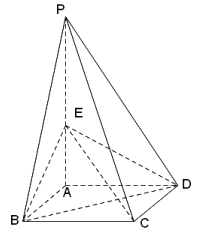
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 分别为
分别为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,过
的中点,过![]() 作平面
作平面![]() 分别与交
分别与交![]() 于点
于点![]() .
.
(Ⅰ)当![]() 为
为![]() 中点时,求证:平面
中点时,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2)![]()
【解析】试题分析:(Ⅰ)要证明面面垂直,即证明线面垂直,根据条件可知![]() ,根据条件易证明
,根据条件易证明![]() ,那么
,那么![]() ,所以
,所以![]() 平面
平面![]() ,就证明了面面垂直;(Ⅱ)根据等体积转化
,就证明了面面垂直;(Ⅱ)根据等体积转化![]() .
.
试题解析:

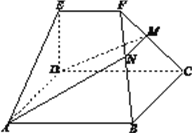
解:(Ⅰ)![]() 为
为![]() 中点,所以四边形
中点,所以四边形![]() 为矩形,所以
为矩形,所以![]() 当
当![]() 时,
时, ![]() 为
为![]() 中点,
中点, ![]() 所以
所以![]()
因为平面![]() ⊥平面
⊥平面![]() ,
, ![]() ,所以
,所以![]()
因为![]() 在面
在面![]() 上,所以
上,所以![]() 所以
所以![]() ⊥面
⊥面![]()
所以面![]() ⊥面
⊥面![]()
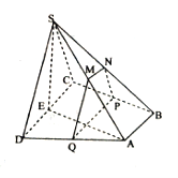
(Ⅱ)![]()
∵![]() ,
, ![]() 为
为![]() 中点 ∴
中点 ∴![]()
又∵平面![]() ⊥平面
⊥平面![]() , 平面
, 平面![]() ∩平面
∩平面![]() ,
, ![]() 在平面
在平面![]() 内
内
∴![]() ∴
∴![]() 即为
即为![]() 到平面
到平面![]() 的距离,即
的距离,即![]()
在![]() 中,
中, ![]() ∴
∴![]()
在直角梯形![]() 中,易求得:
中,易求得: ![]()
∵![]() 为中点 ∴
为中点 ∴![]() ∴
∴![]()
又∵平面![]() ∩平面
∩平面![]()
![]() ∴
∴![]() ,
,
又![]()
∴![]()
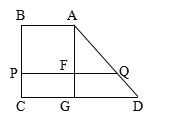 如图,在梯形
如图,在梯形![]() 中,
中, ![]() ,
,![]()
∴![]() ,
, ![]()
![]()
所以三棱锥![]() 的体积
的体积![]() .
.

练习册系列答案
相关题目