题目内容
已知函数f(x)=sinx+λcosx的图象的一个对称中心是点(
,0),则函数g(x)=λsinxcosx+sin2x的图象的一条对称轴是直线( )
| π |
| 3 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=-
|
考点:两角和与差的正弦函数,正弦函数的对称性
专题:三角函数的求值
分析:由对称中心可得λ=-
,代入g(x)由三角函数公式化简可得g(x)=
-sin(2x+
),令2x+
=kπ+
解x可得对称轴,对照选项可得.
| 3 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
解答:
解:∵f(x)=sinx+λcosx的图象的一个对称中心是点(
,0),
∴f(
)=sin
+λcos
=
+
λ=0,解得λ=-
,
∴g(x)=-
sinxcosx+sin2x
=-
sin2x+
=
-sin(2x+
),
令2x+
=kπ+
可得x=
+
,k∈Z,
∴函数的对称轴为x=
+
,k∈Z,
结合四个选项可知,当k=-1时x=-
符合题意,
故选:D
| π |
| 3 |
∴f(
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
∴g(x)=-
| 3 |
=-
| ||
| 2 |
| 1-cos2x |
| 2 |
=
| 1 |
| 2 |
| π |
| 6 |
令2x+
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 6 |
∴函数的对称轴为x=
| kπ |
| 2 |
| π |
| 6 |
结合四个选项可知,当k=-1时x=-
| π |
| 3 |
故选:D
点评:本题考查两角和与差的三角函数,涉及三角函数对称性,属中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
一个几何体的正视图和侧视图都是矩形,俯视图是一个圆(如图所示),该几何体的体积为( )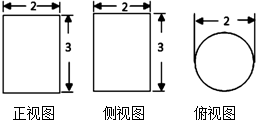

| A、π | B、2π | C、3π | D、4π |
若某程序图如图所示,则该程序运行后输出的k的值是( )


| A、4 | B、5 | C、6 | D、7 |
要得到函数y=cosx的图象,只需要将函数y=cos(x-
)的图象( )
| π |
| 3 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
若不等式
≤μ≤
对任意的t∈(0,2]上恒成立,则μ的取值范围是( )
| t |
| t2+9 |
| ||
t+
|
A、[
| ||||||
B、[
| ||||||
C、[
| ||||||
D、[
|
设集合A={x|y=ln(x+1)},B={-2,-1,0,1},则(∁RA)∩B=( )
| A、{-2} |
| B、{-2,-1} |
| C、{-2,-1,0} |
| D、{-2,-1,0,1} |