题目内容
(本小题满分12分)如图,四棱锥 中,
中,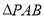 是正三角形,四边形
是正三角形,四边形 是矩形,且平面
是矩形,且平面
 平面
平面 ,
, ,
,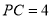 .
.
(Ⅰ)若点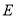 是
是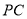 的中点,求证:
的中点,求证: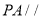 平面
平面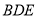 ;
;
(Ⅱ)若点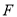 在线段
在线段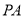 上,且
上,且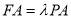 ,当三棱锥
,当三棱锥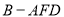 的体积为
的体积为 时,求实数
时,求实数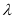 的值.
的值.
(Ⅰ)证明见解析;(Ⅱ)
【解析】
试题分析:(Ⅰ)将证明线面平行转化为线线平行,通过做辅助线可证明出 //
// ,线面平行的判定定理可证出
,线面平行的判定定理可证出 平面
平面 ;(Ⅱ)如图所示作辅助线,通过题意可先分
;(Ⅱ)如图所示作辅助线,通过题意可先分 将问题转化为求
将问题转化为求 ,由面面垂直的性质定理得
,由面面垂直的性质定理得
 平面
平面 ,进而
,进而
 平面
平面 ,得到
,得到
 平面
平面 ,故
,故 ,进而确定
,进而确定 ,再由
,再由
试题解析:(Ⅰ)如图,连接 ,设
,设 ,又点
,又点 是
是 的中点,
的中点,
则在 中,中位线
中,中位线 //
// , 3分
, 3分
又 平面
平面 ,
, 平面
平面 .
.
所以 平面
平面 5分
5分


(Ⅱ)依据题意可得: ,取
,取 中点
中点 ,所以
,所以 ,且
,且
又平面
 平面
平面 ,则
,则
 平面
平面 ; 6分
; 6分
作 于
于 上一点
上一点 ,则
,则
 平面
平面 ,
,
因为四边形 是矩形,所以
是矩形,所以
 平面
平面 ,
,
则 为直角三角形 8分
为直角三角形 8分
所以 ,则直角三角形
,则直角三角形 的面积为
的面积为
 10分
10分
由 得:
得: 12分
12分
考点:1、线面平行问题与线线平行问题的互化;2、面面垂直与线面垂直问题的互化;3、综合分析能力.

(本小题满分12分)心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否据此判断有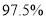 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)经过多次测试后,甲每次解答一道几何题所用的时间在5~7分钟,乙每次解答一道几何题所用的时
间在6~8分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
(3)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为 ,求
,求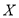 的分布列及数学期望
的分布列及数学期望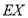 .
.
下面临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
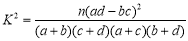 .
.


 为虚数单位,则
为虚数单位,则 =( )
=( ) C.
C.  D.
D. 
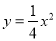 的焦点为
的焦点为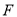 ,定点
,定点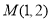 ,点
,点 为抛物线上的动点,则
为抛物线上的动点,则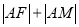 的最小值为( )
的最小值为( ) B.
B.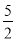 C.
C.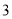 D.
D.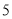
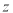 是复数,
是复数,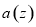 表示满足
表示满足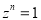 的最小正整数
的最小正整数 ,则对虚数单位
,则对虚数单位 ,
,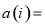 ( )
( ) 满足
满足 ,则目标函数
,则目标函数 的最小值为 .
的最小值为 .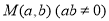 是圆
是圆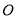 :
: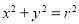 内一点,现有以
内一点,现有以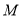 为中点的弦所在
为中点的弦所在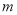 和直线
和直线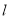 :
: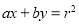 ,则( ).
,则( ).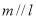 ,且
,且 ,且
,且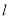 的参数方程为
的参数方程为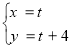 (t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为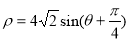 ,则直线
,则直线 和曲线C的公共点有 个.
和曲线C的公共点有 个. 名学生负责校内
名学生负责校内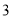 个不同地段的卫生工作,每个地段至少有
个不同地段的卫生工作,每个地段至少有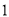 名学生的分配方案共有( )
名学生的分配方案共有( )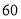 种 B.
种 B.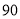 种 C.
种 C.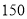 种 D.
种 D.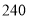 种
种