题目内容
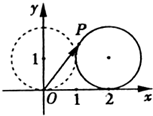 (2012•山东)如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,
(2012•山东)如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,| OP |
(2-sin2,1-cos2)
(2-sin2,1-cos2)
.分析:设滚动后圆的圆心为O',切点为A,连接O'P.过O'作与x轴正方向平行的射线,交圆O'于B(3,1),设∠BO'P=θ,则根据圆的参数方程,得P的坐标为(2+cosθ,1+sinθ),再根据圆的圆心从(0,1)滚动到(2,1),算出θ=
-2,结合三角函数的诱导公式,化简可得P的坐标为(2-sin2,1-cos2),即为向量
的坐标.
| 3π |
| 2 |
| OP |
解答: 解:设滚动后的圆的圆心为O',切点为A(2,0),连接O'P,
解:设滚动后的圆的圆心为O',切点为A(2,0),连接O'P,
过O'作与x轴正方向平行的射线,交圆O'于B(3,1),设∠BO'P=θ
∵⊙O'的方程为(x-2)2+(y-1)2=1,
∴根据圆的参数方程,得P的坐标为(2+cosθ,1+sinθ),
∵单位圆的圆心的初始位置在(0,1),圆滚动到圆心位于(2,1)
∴∠AO'P=2,可得θ=
-2
可得cosθ=cos(
-2)=-sin2,sinθ=sin(
-2)=-cos2,
代入上面所得的式子,得到P的坐标为(2-sin2,1-cos2)
∴
的坐标为(2-sin2,1-cos2).
故答案为:(2-sin2,1-cos2)
 解:设滚动后的圆的圆心为O',切点为A(2,0),连接O'P,
解:设滚动后的圆的圆心为O',切点为A(2,0),连接O'P,过O'作与x轴正方向平行的射线,交圆O'于B(3,1),设∠BO'P=θ
∵⊙O'的方程为(x-2)2+(y-1)2=1,
∴根据圆的参数方程,得P的坐标为(2+cosθ,1+sinθ),
∵单位圆的圆心的初始位置在(0,1),圆滚动到圆心位于(2,1)
∴∠AO'P=2,可得θ=
| 3π |
| 2 |
可得cosθ=cos(
| 3π |
| 2 |
| 3π |
| 2 |
代入上面所得的式子,得到P的坐标为(2-sin2,1-cos2)
∴
| OP |
故答案为:(2-sin2,1-cos2)
点评:本题根据半径为1的圆的滚动,求一个向量的坐标,着重考查了圆的参数方程和平面向量的坐标表示的应用等知识点,属于中档题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
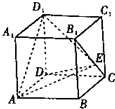 (2012•山东)如图,正方体ABCD-A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A-DED1的体积为
(2012•山东)如图,正方体ABCD-A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A-DED1的体积为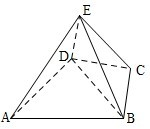 (2012•山东)如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
(2012•山东)如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD. (2012•山东)如图,椭圆
(2012•山东)如图,椭圆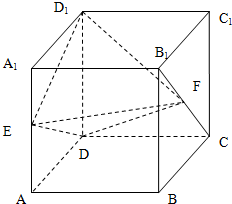 (2012•山东)如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为
(2012•山东)如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为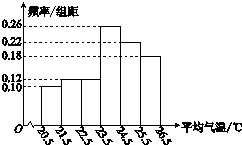 (2012•山东)如图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为[20.5,21.5),[21.5,22.5),[22.5,23.5),[23.5,24.5),[24.5,25.5),[25.5,26.5].已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为
(2012•山东)如图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为[20.5,21.5),[21.5,22.5),[22.5,23.5),[23.5,24.5),[24.5,25.5),[25.5,26.5].已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为