题目内容
 (2012•山东)如图,椭圆M:
(2012•山东)如图,椭圆M:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆M的标准方程;
(Ⅱ)设直线l:y=x+m(m∈R)与椭圆M有两个不同的交点P,Q,l与矩形ABCD有两个不同的交点S,T.求
| |PQ| |
| |ST| |
分析:(Ⅰ)通过椭圆的离心率,矩形的面积公式,直接求出a,b,然后求椭圆M的标准方程;
(Ⅱ) 通过
⇒5x2+8mx+4m2-4=0,利用韦达定理求出|PQ|的表达式,通过判别式推出的m的范围,①当-
<m<-1时,求出
取得最大值
.利用由对称性,推出1<m<
,
取得最大值
.③当-1≤m≤1时,
取得最大值
.求
的最大值及取得最大值时m的值.
(Ⅱ) 通过
|
| 5 |
| |PQ| |
| |ST| |
| 2 |
| 5 |
| 5 |
| 5 |
| |PQ| |
| |ST| |
| 2 |
| 5 |
| 5 |
| |PQ| |
| |ST| |
| 2 |
| 5 |
| 5 |
| |PQ| |
| |ST| |
解答:解:(I)e=
=
⇒
=
…①
矩形ABCD面积为8,即2a•2b=8…②
由①②解得:a=2,b=1,
∴椭圆M的标准方程是
+y2=1.
(II)
⇒5x2+8mx+4m2-4=0,
由△=64m2-20(4m2-4)>0得-
<m<
.
设P(x1,y1),Q(x2,y2),则x1+x2=-
m,x1x2=
,
|PQ|=
=
.
当l过A点时,m=1,当l过C点时,m=-1.
①当-
<m<-1时,有S(-m-1,-1),T(2,2+m),|ST|=
(3+m),
=
=
,
其中t=m+3,由此知当
=
,即t=
,m=-
∈(-
,-1)时,
取得最大值
.
②由对称性,可知若1<m<
,则当m=
时,
取得最大值
.
③当-1≤m≤1时,|ST|=2
,
=
,
由此知,当m=0时,
取得最大值
.
综上可知,当m=±
或m=0时,
取得最大值
.
| c |
| a |
| ||
| 2 |
| a2-b2 |
| a2 |
| 3 |
| 4 |
矩形ABCD面积为8,即2a•2b=8…②
由①②解得:a=2,b=1,
∴椭圆M的标准方程是
| x2 |
| 4 |
(II)
|
由△=64m2-20(4m2-4)>0得-
| 5 |
| 5 |
设P(x1,y1),Q(x2,y2),则x1+x2=-
| 8 |
| 5 |
| 4m2-4 |
| 5 |
|PQ|=
| 2 |
(-
|
4
| ||
| 5 |
| 5-m2 |
当l过A点时,m=1,当l过C点时,m=-1.
①当-
| 5 |
| 2 |
| |PQ| |
| |ST| |
| 4 |
| 5 |
|
| 4 |
| 5 |
-
|
其中t=m+3,由此知当
| 1 |
| t |
| 3 |
| 4 |
| 4 |
| 3 |
| 5 |
| 3 |
| 5 |
| |PQ| |
| |ST| |
| 2 |
| 5 |
| 5 |
②由对称性,可知若1<m<
| 5 |
| 5 |
| 3 |
| |PQ| |
| |ST| |
| 2 |
| 5 |
| 5 |
③当-1≤m≤1时,|ST|=2
| 2 |
| |PQ| |
| |ST| |
| 2 |
| 5 |
| 5-m2 |
由此知,当m=0时,
| |PQ| |
| |ST| |
| 2 |
| 5 |
| 5 |
综上可知,当m=±
| 5 |
| 3 |
| |PQ| |
| |ST| |
| 2 |
| 5 |
| 5 |
点评:本题考查椭圆的标准方程,直线与圆锥曲线的综合问题,考查分类讨论思想,转化思想,韦达定理以及判别式的应用,设而不求的解题方法,考查分析问题解决问题,计算能力.

练习册系列答案
相关题目
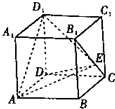 (2012•山东)如图,正方体ABCD-A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A-DED1的体积为
(2012•山东)如图,正方体ABCD-A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A-DED1的体积为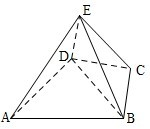 (2012•山东)如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
(2012•山东)如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.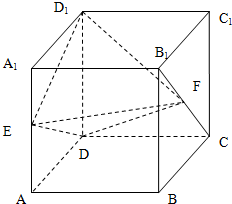 (2012•山东)如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为
(2012•山东)如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为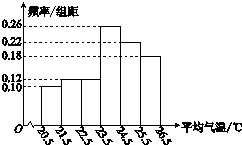 (2012•山东)如图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为[20.5,21.5),[21.5,22.5),[22.5,23.5),[23.5,24.5),[24.5,25.5),[25.5,26.5].已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为
(2012•山东)如图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为[20.5,21.5),[21.5,22.5),[22.5,23.5),[23.5,24.5),[24.5,25.5),[25.5,26.5].已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为