题目内容
已知函数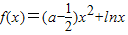 .(a∈R)
.(a∈R)(1)当a=1时,求f(x)在区间[1,e]上的最大值和最小值;
(2)若在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax下方,求a的取值范围.
【答案】分析:(1)求出函数的导函数判断出其大于零得到函数在区间[1,e]上为增函数,所以f(1)为最小值,f(e)为最大值,求出即可;(2)令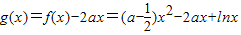 ,则g(x)的定义域为(0,+∞).证g(x)<0在区间(1,+∞)上恒成立即得证.求出g′(x)分区间讨论函数的增减性得到函数的极值,利用极值求出a的范围即可.
,则g(x)的定义域为(0,+∞).证g(x)<0在区间(1,+∞)上恒成立即得证.求出g′(x)分区间讨论函数的增减性得到函数的极值,利用极值求出a的范围即可.
解答:解(Ⅰ)当a=1时,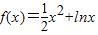 ,
,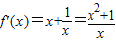 .
.
对于x∈[1,e],有f'(x)>0,∴f(x)在区间[1,e]上为增函数.
∴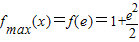 ,
,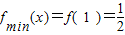
(Ⅱ)令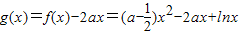 ,则g(x)的定义域为(0,+∞).
,则g(x)的定义域为(0,+∞).
在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax下方等价于g(x)<0在区间(1,+∞)上恒成立.
∵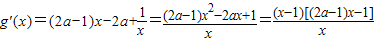 .
.
①若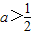 ,令g'(x)=0,得极值点x1=1,
,令g'(x)=0,得极值点x1=1,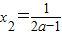 .
.
当x2>x1=1,即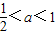 时,在(x2,+∞)上有g'(x)>0.
时,在(x2,+∞)上有g'(x)>0.
此时g(x)在区间(x2,+∞)上是增函数,并且在该区间上有g(x)∈(g(x2),+∞),不合题意;
当x2<x1=1,即a≥1时,同理可知,g(x)在区间(1,+∞)上,有g(x)∈(g(1),+∞),也不合题意;
②若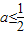 ,则有2a-1≤0,此时在区间(1,+∞)上恒有g'(x)<0.
,则有2a-1≤0,此时在区间(1,+∞)上恒有g'(x)<0.
从而g(x)在区间(1,+∞)上是减函数
要使g(x)<0在此区间上恒成立,只须满足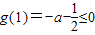
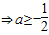 .
.
由此求得a的范围是[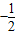 ,
, ].
].
综合①②可知,当a∈[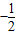 ,
, ]时,函数f(x)的图象恒在直线y=2ax下方.
]时,函数f(x)的图象恒在直线y=2ax下方.
点评:考查学生利用导数求函数在闭区间上的最值的能力.以及综合运用函数解决数学问题的能力.
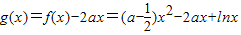 ,则g(x)的定义域为(0,+∞).证g(x)<0在区间(1,+∞)上恒成立即得证.求出g′(x)分区间讨论函数的增减性得到函数的极值,利用极值求出a的范围即可.
,则g(x)的定义域为(0,+∞).证g(x)<0在区间(1,+∞)上恒成立即得证.求出g′(x)分区间讨论函数的增减性得到函数的极值,利用极值求出a的范围即可.解答:解(Ⅰ)当a=1时,
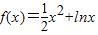 ,
,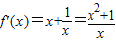 .
.对于x∈[1,e],有f'(x)>0,∴f(x)在区间[1,e]上为增函数.
∴
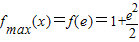 ,
,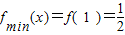
(Ⅱ)令
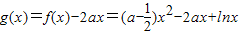 ,则g(x)的定义域为(0,+∞).
,则g(x)的定义域为(0,+∞).在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax下方等价于g(x)<0在区间(1,+∞)上恒成立.
∵
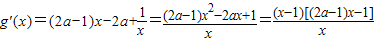 .
.①若
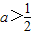 ,令g'(x)=0,得极值点x1=1,
,令g'(x)=0,得极值点x1=1,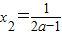 .
.当x2>x1=1,即
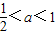 时,在(x2,+∞)上有g'(x)>0.
时,在(x2,+∞)上有g'(x)>0.此时g(x)在区间(x2,+∞)上是增函数,并且在该区间上有g(x)∈(g(x2),+∞),不合题意;
当x2<x1=1,即a≥1时,同理可知,g(x)在区间(1,+∞)上,有g(x)∈(g(1),+∞),也不合题意;
②若
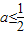 ,则有2a-1≤0,此时在区间(1,+∞)上恒有g'(x)<0.
,则有2a-1≤0,此时在区间(1,+∞)上恒有g'(x)<0.从而g(x)在区间(1,+∞)上是减函数
要使g(x)<0在此区间上恒成立,只须满足
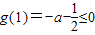
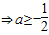 .
.由此求得a的范围是[
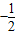 ,
, ].
].综合①②可知,当a∈[
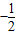 ,
, ]时,函数f(x)的图象恒在直线y=2ax下方.
]时,函数f(x)的图象恒在直线y=2ax下方.点评:考查学生利用导数求函数在闭区间上的最值的能力.以及综合运用函数解决数学问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,其中a∈R.
,其中a∈R.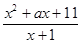 (a∈R),若对于任意的X∈N*,f(x)≥3恒成立,则a的取值范围是___
(a∈R),若对于任意的X∈N*,f(x)≥3恒成立,则a的取值范围是___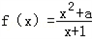 (其中a∈R).
(其中a∈R).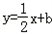 ,求实数a,b的值;
,求实数a,b的值;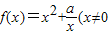 ,常数a∈R),若函数f(x)在x∈[2,+∞)上是增函数,则a的取值范围是 .
,常数a∈R),若函数f(x)在x∈[2,+∞)上是增函数,则a的取值范围是 .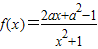 ,其中a∈R.
,其中a∈R.