题目内容
设a∈R,若关于x的不等式|cos2x|≥asinx在区间[-
,
]上恒成立,则实数a的取值范围是( )
| π |
| 3 |
| π |
| 6 |
A、[-
| ||||||
B、[-
| ||||||
C、[0,
| ||||||
| D、{0} |
考点:三角函数线
专题:三角函数的求值
分析:设sinx=t,则:|2t2-1|≥at,其中t∈[-
,
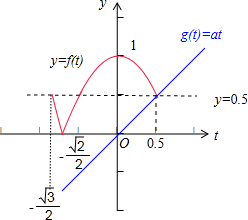
].作出f(t)=|2t2-1|的图象,再作出g(t)=at的图象,此题就是解不等式f(t)≥g(t),结合图象可得a的范围
| ||
| 2 |
| 1 |
| 2 |
解答:
 解:关于x的不等式|cos2x|≥asinx在
解:关于x的不等式|cos2x|≥asinx在
区间[-
,
]上恒成立,
故|1-2sin2x|≥asinx在闭区间[-
,
]上恒成立,
设sinx=t,则:|2t2-1|≥at,其中t∈[-
,
].
作出f(t)=|2t2-1|在区间[-
,
]上的图象,
再作出g(t)=at在区间∈[-
,
]上的图象,
此题就是不等式f(t)≥g(t)当t∈[-
,
]时恒成立,
结合图象可得:a∈[0,1],
故选:D.
 解:关于x的不等式|cos2x|≥asinx在
解:关于x的不等式|cos2x|≥asinx在区间[-
| π |
| 3 |
| π |
| 6 |
故|1-2sin2x|≥asinx在闭区间[-
| π |
| 3 |
| π |
| 6 |
设sinx=t,则:|2t2-1|≥at,其中t∈[-
| ||
| 2 |
| 1 |
| 2 |
作出f(t)=|2t2-1|在区间[-
| ||
| 2 |
| 1 |
| 2 |
再作出g(t)=at在区间∈[-
| ||
| 2 |
| 1 |
| 2 |
此题就是不等式f(t)≥g(t)当t∈[-
| ||
| 2 |
| 1 |
| 2 |
结合图象可得:a∈[0,1],
故选:D.
点评:本题考查同角三角函数的基本关系,正弦函数的定义域和值域,二次函数的性质,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
相关题目