题目内容
经过点M(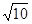 ,0)作直线l,交曲线
,0)作直线l,交曲线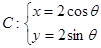 (θ为参数)于A,B两点,若|MA|,|AB|,|MB|成等比数列,求直线l的方程.
(θ为参数)于A,B两点,若|MA|,|AB|,|MB|成等比数列,求直线l的方程.
 或
或 .
.
解析试题分析:先将直线设为 代入曲线C,得到关于t的方程,利用t的几何意义,利用|MA|,|AB|,|MB|成等比数列,得到
代入曲线C,得到关于t的方程,利用t的几何意义,利用|MA|,|AB|,|MB|成等比数列,得到 ,可以求出方程.
,可以求出方程.
试题解析:解:根据题意,设直线l的参数方程为 (t为参数)
(t为参数)
曲线C 化成普通方程得x2+y2=4.
化成普通方程得x2+y2=4.
将 代入
代入 得
得
(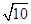 +tcosθ)2+t2sin2θ=4.
+tcosθ)2+t2sin2θ=4.
化简整理得t2+2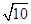 cosθt+6=0,
cosθt+6=0,
∴t1+t2=-2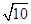 cosθ,t1t2=6.
cosθ,t1t2=6.
由题意得|AB|2=|MA||MB|,
而|AB|2=(t1-t2)2=(t1+t2)2-4t1t2,
|MA||MB|=|t1t2|=6,
即40cos2θ-24=6,解得cosθ=± ,
,
∴sinθ= ,k=tanθ=±
,k=tanθ=± .
.
所求直线l的方程为 或
或 .
.
考点:1.参数方程与普通方程的互化;2.弦长公式.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 中,过椭圆
中,过椭圆 的右焦点,且与直线
的右焦点,且与直线 (
( 为参数)平行的直线截椭圆所得弦长为 .
为参数)平行的直线截椭圆所得弦长为 . ,点
,点 在直线
在直线 上运动,当线段
上运动,当线段 最短时,点
最短时,点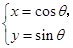 (
(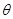 为参数),曲线C2:
为参数),曲线C2: (t为参数).
(t为参数).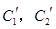 .写出
.写出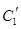 与
与 公共点的个数和C
公共点的个数和C 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.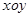 中,曲线
中,曲线 的参数方程为
的参数方程为 ,(
,( 为参数),以原点
为参数),以原点 为极点,
为极点, 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
. 为曲线
为曲线 上的动点,求点
上的动点,求点 中,已知直线
中,已知直线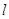 的参数方程
的参数方程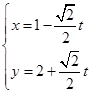 (
(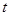 为参数),直线
为参数),直线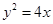 相交于
相交于 两点,求线段
两点,求线段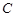 的参数方程为
的参数方程为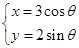 (
(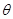 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线 上的点按坐标变换
上的点按坐标变换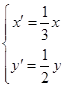 得到曲线
得到曲线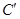 .
. 在曲线
在曲线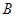
 ,当点
,当点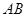 中点
中点 的轨迹方程.
的轨迹方程.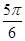 .
.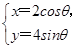 (θ为参数)交于A,B两点,求|PA|·|PB|.
(θ为参数)交于A,B两点,求|PA|·|PB|. 中,曲线
中,曲线 的参数方程为
的参数方程为 ,
, 为极点,
为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
. 时,曲线
时,曲线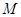 、
、 两点,求以线段
两点,求以线段 为直径的圆的直角坐标方程.
为直径的圆的直角坐标方程.