题目内容
如图所示，直角坐标系xOy建立在湖泊的某一恰当位置，现准备在湖泊的一侧修建一条观光大道，它的前一段MD是以O为圆心，OD为半径的圆弧，后一段DBC是函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜| π |
| 2 |
| 8 |
| 3 |
（Ⅰ）求函数y=sin（ωx+φ）的解析式；
（Ⅱ）若在湖泊内修建如图所示的矩形水上乐园OEPF，其中折线FPE为水上赛艇线路，问点P落在圆弧MD上何处时赛艇线路最长？
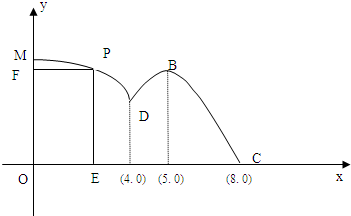
分析：（I）函数y=f（x）的相邻两条对称轴间距离，求出函数周期，得到ω，函数的图象的一个对称中心，求出φ，然后求出函数y=f（x）的解析式；
（II）在y=
sin(
x-
) 中令x=4，得OD，再连接OP，设赛艇线路长为L．利用三角函数表示出来L，再利用三角函数的性质求得L 有最大值即可解决问题．
（II）在y=
| 8 |
| 3 |
| π |
| 6 |
| π |
| 3 |
解答：解：（I）对于函数y=Asin（ωx+φ），
由图象知，A=
，ω=
=
=
…（3分）
将B(5，
) 代入到y=
sin(
x+φ) 中，得
x+φ=2kπ+
，(k∈Z)，又|φ|＜
，
所以φ=-
，故y=
sin(
x-
) …（7分）
（II）在y=
sin(
x-
) 中令x=4，得D(4，
)
∴OD=
…（9分）
连接OP，设∠EOP=θ，θ∈[
，
)，则P(
cosθ，
sinθ)
设赛艇线路长为L．
则L=PE+PF=
cosθ+
sinθ=
sin(θ+
) …（12分）
当θ=
时L 有最大值
，此时P(
，
)．…（14分）
所以当P 点的坐标为(
，
) 时赛艇线路最长．′…（15分）
由图象知，A=
| 8 |
| 3 |
| 2π |
| T |
| 2 |
| 4(8-5) |
| π |
| 6 |
将B(5，
| 8 |
| 3 |
| 8 |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 2 |
| π |
| 2 |
所以φ=-
| π |
| 3 |
| 8 |
| 3 |
| π |
| 6 |
| π |
| 3 |
（II）在y=
| 8 |
| 3 |
| π |
| 6 |
| π |
| 3 |
4
| ||
| 3 |
∴OD=
8
| ||
| 3 |
连接OP，设∠EOP=θ，θ∈[
| π |
| 6 |
| π |
| 2 |
8
| ||
| 3 |
8
| ||
| 3 |
设赛艇线路长为L．
则L=PE+PF=
8
| ||
| 3 |
8
| ||
| 3 |
8
| ||
| 3 |
| π |
| 4 |
当θ=
| π |
| 4 |
8
| ||
| 3 |
4
| ||
| 3 |
4
| ||
| 3 |
所以当P 点的坐标为(
4
| ||
| 3 |
4
| ||
| 3 |
点评：题是基础题，考查三角函数的解析式的求法，注意周期的应用，两角和的余弦公式的应用，同时注意角的范围，以及角的变换的技巧，是解题的关键，考查计算能力．
练习册系列答案
相关题目
在如图所示的直角坐标系中，B为单位圆在第一象限内圆弧上的动点，A（1，0），设
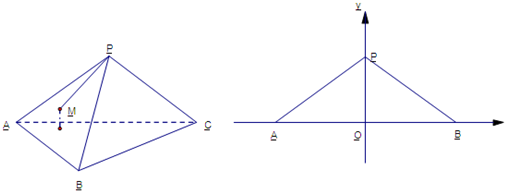
有一矩形钢板ABCD缺损了一角（图中阴影部分），边缘线OM上每一点到点D的距离都等于它到边AB的距离．工人师傅要将缺损的一角切割下来使剩余部分成一个五边形，已知AB=4米，AD=2米．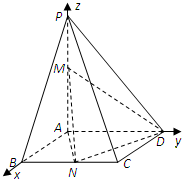
在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PA⊥面ABCD，PA=2，点M，N分别为边PA，BC的中点．建立如图所示的直角坐标系A-xyz．
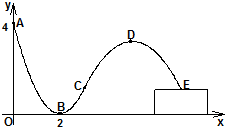轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动．如图，助跑道ABC是一段抛物线，某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1米的平台上E处，飞行的轨迹是一段抛物线CDE（抛物线CDE与抛物线ABC在同一平面内），D为这段抛物线的最高点．现在运动员的滑行轨迹所在平面上建立如图所示的直角坐标系，x轴在地面上，助跑道一端点A（0，4），另一端点C（3，1），点B（2，0），单位：米．